题目内容
已知函数f(x)=x2-4ax+2a+6,x∈R.
(1)若函数的值域为[0,+∞),求a的值;
(2)若函数的值域为非负数集,求函数f(a)=2-a|a+3|的值域.
(1)若函数的值域为[0,+∞),求a的值;
(2)若函数的值域为非负数集,求函数f(a)=2-a|a+3|的值域.
(1)a=-1或a=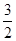
(2)[-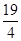 ,4]
,4]
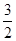
(2)[-
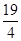 ,4]
,4]解:f(x)=x2-4ax+2a+6=(x-2a)2+2a+6-4a2.
(1)∵函数值域为[0,+∞),∴2a+6-4a2=0.
解得a=-1或a=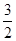 .
.
(2)∵函数值域为非负数集,∴2a+6-4a2≥0.
即2a2-a-3≤0,解得-1≤a≤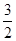 .
.
∴f(a)=2-a|a+3|=2-a(a+3)=-(a+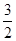 )2+
)2+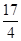 .
.
∴f(a)在[-1,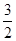 ]上单调递减.
]上单调递减.
∴-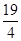 ≤f(a)≤4.
≤f(a)≤4.
即f(a)值域为[-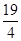 ,4].
,4].
(1)∵函数值域为[0,+∞),∴2a+6-4a2=0.
解得a=-1或a=
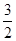 .
.(2)∵函数值域为非负数集,∴2a+6-4a2≥0.
即2a2-a-3≤0,解得-1≤a≤
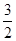 .
.∴f(a)=2-a|a+3|=2-a(a+3)=-(a+
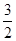 )2+
)2+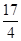 .
.∴f(a)在[-1,
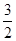 ]上单调递减.
]上单调递减.∴-
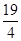 ≤f(a)≤4.
≤f(a)≤4.即f(a)值域为[-
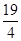 ,4].
,4].
练习册系列答案
相关题目
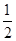 ex(sinx+cosx)在区间[0,
ex(sinx+cosx)在区间[0,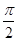 ]上的值域为( )
]上的值域为( )
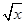 +1,h(x)=
+1,h(x)=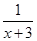 ,x∈(-3,a],其中a为常数且a>0,令函数f(x)=g(x)·h(x).
,x∈(-3,a],其中a为常数且a>0,令函数f(x)=g(x)·h(x).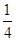 时,求函数f(x)的值域.
时,求函数f(x)的值域.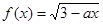 在区间
在区间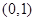 是减函数,则实数
是减函数,则实数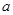 的取值范围是 .
的取值范围是 .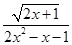 的定义域是________.
的定义域是________.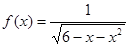 的定义域是________.
的定义域是________.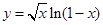 的定义域为( )
的定义域为( )