题目内容
关于平面向量的数量积运算与实数的乘法运算相类比,易得下列结论:
①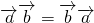 ;②
;②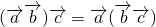 ;③
;③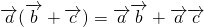 ;
;
④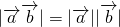 ;⑤由
;⑤由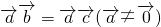 ,可得
,可得 .
.
以上通过类比得到的结论正确的有
- A.2个
- B.3个
- C.4个
- D.5个
A
分析:①根据向量的数量积具有反身性进行判定;② 表示与
表示与 共线的向量,
共线的向量,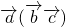 表示与
表示与 共线的向量,
共线的向量, 与
与 不一定共线;③根据向量具有分配律进行判定;④根据向量的数量积公式进行判定;⑤列举反例,当
不一定共线;③根据向量具有分配律进行判定;④根据向量的数量积公式进行判定;⑤列举反例,当 与
与 垂直,
垂直, 与
与 垂直时,不满足条件.
垂直时,不满足条件.
解答:①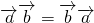 ,向量的数量积具有反身性,故正确;
,向量的数量积具有反身性,故正确;
② 表示与
表示与 共线的向量,
共线的向量,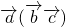 表示与
表示与 共线的向量,
共线的向量, 与
与 不一定共线,故不正确;
不一定共线,故不正确;
③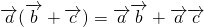 ,向量具有分配律,故正确
,向量具有分配律,故正确
④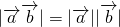 |cosθ|,|cosθ|不一定为1,故不正确;
|cosθ|,|cosθ|不一定为1,故不正确;
⑤当 与
与 垂直,
垂直, 与
与 垂直时,满足条件
垂直时,满足条件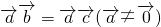 ,但
,但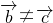 ,故不正确.
,故不正确.
故选A.
点评:本题主要考查了向量数量积的运算法则,同时考查了类比推理,属于中档题.
分析:①根据向量的数量积具有反身性进行判定;②
 表示与
表示与 共线的向量,
共线的向量,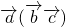 表示与
表示与 共线的向量,
共线的向量, 与
与 不一定共线;③根据向量具有分配律进行判定;④根据向量的数量积公式进行判定;⑤列举反例,当
不一定共线;③根据向量具有分配律进行判定;④根据向量的数量积公式进行判定;⑤列举反例,当 与
与 垂直,
垂直, 与
与 垂直时,不满足条件.
垂直时,不满足条件.解答:①
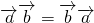 ,向量的数量积具有反身性,故正确;
,向量的数量积具有反身性,故正确;②
 表示与
表示与 共线的向量,
共线的向量,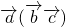 表示与
表示与 共线的向量,
共线的向量, 与
与 不一定共线,故不正确;
不一定共线,故不正确;③
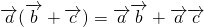 ,向量具有分配律,故正确
,向量具有分配律,故正确④
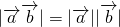 |cosθ|,|cosθ|不一定为1,故不正确;
|cosθ|,|cosθ|不一定为1,故不正确;⑤当
 与
与 垂直,
垂直, 与
与 垂直时,满足条件
垂直时,满足条件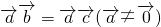 ,但
,但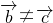 ,故不正确.
,故不正确.故选A.
点评:本题主要考查了向量数量积的运算法则,同时考查了类比推理,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
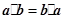 ;②
;②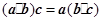 ;③
;③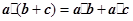 ;
;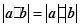 ;⑤由
;⑤由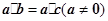 可得
可得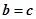 .
.