题目内容
关于平面向量的数量积运算与实数的乘法运算相类比,易得下列结论:
①
•
=
•
;②(
•
)•
=
•(
•
);③
•(
+
)=
•
+
•
;
④|
•
|=|
|•|
|;⑤由
•
=
•
(
≠
),可得
=
.
以上通过类比得到的结论正确的有( )
①
| a |
| b |
| b |
| a |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
④|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| c |
| a |
| 0 |
| b |
| c |
以上通过类比得到的结论正确的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
分析:①根据向量的数量积具有反身性进行判定;②(
•
)•
表示与
共线的向量,
•(
•
)表示与
共线的向量,
与
不一定共线;③根据向量具有分配律进行判定;④根据向量的数量积公式进行判定;⑤列举反例,当
与
垂直,
与
垂直时,不满足条件.
| a |
| b |
| c |
| c |
| a |
| b |
| c |
| a |
| a |
| c |
| a |
| b |
| a |
| c |
解答:解:①
•
=
•
,向量的数量积具有反身性,故正确;
②(
•
)•
表示与
共线的向量,
•(
•
)表示与
共线的向量,
与
不一定共线,故不正确;
③
•(
+
)=
•
+
•
,向量具有分配律,故正确
④|
•
|=|
|•|
||cosθ|,|cosθ|不一定为1,故不正确;
⑤当
与
垂直,
与
垂直时,满足条件
•
=
•
(
≠
),但
≠
,故不正确.
故选A.
| a |
| b |
| b |
| a |
②(
| a |
| b |
| c |
| c |
| a |
| b |
| c |
| a |
| a |
| c |
③
| a |
| b |
| c |
| a |
| b |
| a |
| c |
④|
| a |
| b |
| a |
| b |
⑤当
| a |
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
| 0 |
| b |
| c |
故选A.
点评:本题主要考查了向量数量积的运算法则,同时考查了类比推理,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
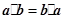 ;②
;②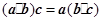 ;③
;③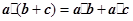 ;
;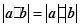 ;⑤由
;⑤由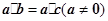 可得
可得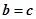 .
.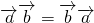 ;②
;②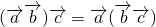 ;③
;③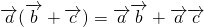 ;
;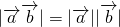 ;⑤由
;⑤由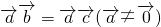 ,可得
,可得 .
.