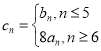题目内容
【题目】已知公差不为零的等差数列{an}的前n项和为Sn,S3=15,a1,a4,a13成等比数列.
(1)求数列{an}的通项公式;
(2)求数列![]() 的前n项和Tn大于2020的最小自然数n.
的前n项和Tn大于2020的最小自然数n.
【答案】(1)an=2n+1;(2)10.
【解析】
(1)设等差数列{an}的公差为d(d≠0),由题设条件列出d的方程,解出d,a1,求出通项公式;
(2)由(1)求得a![]() ,再使用分组求和求出Tn,研究其单调性,求出满足Tn大于2020的最小自然数n.
,再使用分组求和求出Tn,研究其单调性,求出满足Tn大于2020的最小自然数n.
(1)设等差数列{an}的公差为d(d≠0),则S3=3a1![]() 15,
15,
∴a1+d=5,a4=5+2d,a13=5+11d,
∵a1,a4,a13成等比数列,
∴(5+2d)2=(5![]() d)(5+11d),解得d=0(舍去)或d=2,
d)(5+11d),解得d=0(舍去)或d=2,
故a1=5![]() d=3.
d=3.
所以an=3+(n![]() 1)×2=2n+1.
1)×2=2n+1.
(2)根据(1)知a![]() 2(2n
2(2n![]() n)+1=2n+1
n)+1=2n+1![]() (2n
(2n![]() 1),
1),
∴Tn=(22+23+…+2n+1)![]() [1+3+…+(2n
[1+3+…+(2n![]() 1)]
1)]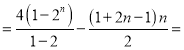 2n+2
2n+2![]() n2
n2![]() 4.
4.
∵2n![]() n>0,
n>0,
∴a![]() 2(2n
2(2n![]() n)+1>0,
n)+1>0,
∴Tn单调递增,
又∵T9<2020,T10>2020,
所以Tn大于2020的最小自然数n为10.
【点晴】
本题主要考查等差数列基本量的运算,数列的分组求和,数列的单调性,属于中档题.

练习册系列答案
相关题目
【题目】已知椭圆![]() :
:![]() (
(![]() ).下面表格所确定的点
).下面表格所确定的点![]() 中,恰有三个点在椭圆
中,恰有三个点在椭圆![]() 上.
上.
|
|
| 1 |
|
|
| 0 |
|
|
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为坐标原点,点
为坐标原点,点![]() ,
,![]() 分别为
分别为![]() 的上下顶点,直线
的上下顶点,直线![]() 经过
经过![]() 的右顶点
的右顶点![]() ,且与
,且与![]() 的另一个公共点为
的另一个公共点为![]() ,直线
,直线![]() ,
,![]() 相交于点
相交于点![]() ,若
,若![]() 与
与![]() 轴的交点
轴的交点![]() 异于
异于![]() ,
,![]() ,证明
,证明![]() 为定值.
为定值.