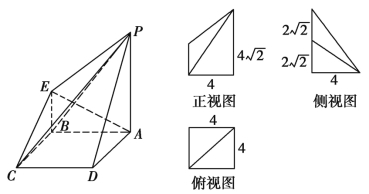
题目内容
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求实数k的值;
(2)设g(x)=log4(a2x+a),若f(x)=g(x)有且只有一个实数解,求实数a的取值范围.
【答案】解:(1)由函数f(x)是偶函数可知:f(x)=f(﹣x),
∴![]() ,化简得
,化简得![]() ,
,
即x=﹣2kx对一切x∈R恒成立,∴k=-![]() .
.
(2)由题意可得,函数f(x)与g(x)的图象有且只有一个公共点,
即方程![]() 有且只有一个实根,
有且只有一个实根,
化简得:方程![]() 有且只有一个实根,且a2x+a>0成立,则a>0.
有且只有一个实根,且a2x+a>0成立,则a>0.
令t=2x>0,则(a﹣1)t2+at﹣1=0有且只有一个正根,
设g(t)=(a﹣1)t2+at﹣1,注意到g(0)=﹣1<0,
所以①当a=1时,有t=1,合题意;
②当0<a<1时,g(t)图象开口向下,且g(0)=﹣1<0,则需满足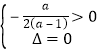 ,
,
此时有a=-2+2![]() ;a=-2-2
;a=-2-2![]() (舍去).
(舍去).
③当a>1时,又g(0)=﹣1,方程恒有一个正根与一个负根.
综上可知,a的取值范围是{-2+2![]() }∪[1,+∞).
}∪[1,+∞).
【解析】(1)由f(x)=f(﹣x),化简可得x=﹣2kx对一切x∈R恒成立,从而求得k的值.
(2)由题意可得,函数f(x)与g(x)的图象有且只有一个公共点,方程![]() 有且只有一个实根,且a2x+a>0成立,则a>0.令t=2x>0,则(a﹣1)t2+at﹣1=0有且只有一个正根,分类讨论求得a的范围,综合可得结论.
有且只有一个实根,且a2x+a>0成立,则a>0.令t=2x>0,则(a﹣1)t2+at﹣1=0有且只有一个正根,分类讨论求得a的范围,综合可得结论.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如下图:
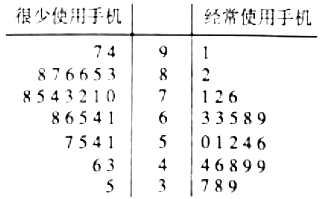
(1)根据茎叶图中的数据完成下面的![]() 列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
及格( | 不及格 | 合计 | |
很少使用手机 | |||
经常使用手机 | |||
合计 |
(2)从50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数列题,甲、乙独立解决此题的概率分别为![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,则此二人适合结为学习上互帮互助的“师徒”,记
,则此二人适合结为学习上互帮互助的“师徒”,记![]() 为两人中解决此题的人数,若
为两人中解决此题的人数,若![]() ,问两人是否适合结为“师徒”?
,问两人是否适合结为“师徒”?
参考公式及数据: 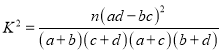 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |