Question

【题目】某工厂拟建一座平面图为矩形，面积为，高度一定的三段污水处理池（如图），由于受地形限制，其长、宽都不超过，如果池的外壁的建造费单价为元，池中两道隔壁墙（与宽边平行）的建造费单价为元，池底的建造费单价为元.设水池的长为，总造价为.

（1）求的表达式；

（2）水池的长与宽各是多少时，总造价最低，并求出这个最低造价.

Answer 1

【答案】（1）；（2）水池长为，宽为，最低造价为元.

【解析】

（1）水池长为，可得其宽为，由其长、宽都不超过可求得的取值范围，根据题意可得出函数的表达式；

（2）利用基本不等式可求得函数的最小值，利用等号成立的条件可求得水池的长与宽，进而得解.

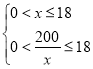（1）水池的长为，则宽为，由题意可得，解得，

，

；

（2），

当且仅当，即时取等号，此时，.

因此，当水池长为，宽为，其总造价最低，最低造价为元.