题目内容
【题目】已知数列{an}中,a1=1,a2=a,且an+1=k(an+an+2)对任意正整数n都成立,数列{an}的前n项和为Sn.
(1)若![]() ,且S2019=2019,求a;
,且S2019=2019,求a;
(2)是否存在实数k,使数列{an}是公比不为1的等比数列,且任意相邻三项am,am+1,am+2按某顺序排列后成等差数列,若存在,求出所有k的值;若不存在,请说明理由;
(3)若![]() ,求Sn.
,求Sn.
【答案】(1) a=1;(2)存在满足要求的实数k有且仅有一个![]()
![]() ;(3) Sn=
;(3) Sn=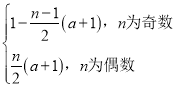
【解析】
(1)由题意求得首项为1,公差d=a-1,结合等差数列前n项和公式列方程可得a;
(2)假设存在满足题意的实数k,分类讨论可得k;
(3)k=![]()
![]() ,an+1=
,an+1=![]()
![]() (an+an+2),an+2+an+1=
(an+an+2),an+2+an+1=![]() (an+1+an),an+3+an+2=
(an+1+an),an+3+an+2=![]() (an+2+an+1)=an+1+an,结合题意分类讨论,然后分组求和可得Sn.
(an+2+an+1)=an+1+an,结合题意分类讨论,然后分组求和可得Sn.
解:(1)k=![]() ,an+1=
,an+1=![]() (an+an+2),
(an+an+2),
∴数列{an}为等差数列,
∵a1=1,a2=a,∴公差d=a-1,
∴S2019=2019=2019+![]() ×(a-1),解得a=1;
×(a-1),解得a=1;
(2)设数列{an}是公比不为1的等比数列,则它的公比q=![]() =a,
=a,
∴am=am-1,am+1=am,am+2=am+1,任意相邻三项
am,am+1,am+2按某顺序排列后成等差数列,
①an+1为等差中项,则2am+1=am+am+2.
即am-1+am+1=2am,解得a=1,不合题意;
②am为等差中项,则2am=am+1+am+2,
即2am-1=am+1+am,化简a2+a-2=0,解得a=-2或a=1(舍去);
③若am+2为等差中项,则2am+2=am+1+am,
即2am+1=am+am-1,化简得:2a2-a-1=0,解得a=![]()
![]() ;
;
∴k=![]() =
=![]() =
=![]() =
=![]()
![]() .
.
综上可得,满足要求的实数k有且仅有一个![]()
![]() ;
;
(3)k=![]()
![]() ,则an+1=
,则an+1=![]()
![]() (an+an+2),
(an+an+2),
∴an+2+an+1=![]() (an+1+an),an+3+an+2=
(an+1+an),an+3+an+2=![]() (an+2+an+1)=an+1+an,
(an+2+an+1)=an+1+an,
当n是偶数时,Sn=a1+a2+…+an=(a1+a2)+…+(an-1+an)
=![]() (a1+a2)=
(a1+a2)=![]() (a+1).
(a+1).
当n是奇数时,Sn=a1+(a2+a3)+…+(an-1+an)
=1+![]() (a2+a3)=1+
(a2+a3)=1+![]() [-(a1+a2)]=1
[-(a1+a2)]=1![]()
![]() (a+1)(n≥1),
(a+1)(n≥1),
n=1也适合上式,
综上可得,Sn=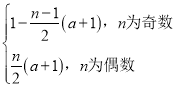 .
.