题目内容
（本小题满分12分）光线l过点P(1，－1)，经y轴反射后与圆C:(x－4)2+(y－4)2=1
相切，求光线l所在的直线方程.
【答案】
解：设l与y轴的交点(即反射点)为Q,点P关于y轴的对称点为P′(－1，－1).由
光学知识可知直线P′Q为反射线所在的直线，且为圆C的切线. ………………………2分
设P′Q的方程为y+1=k(x+1)，即kx－y+k－1=0, …………………………………4分
由于圆心C(4，4)到P′Q的距离等于半径长，
∴
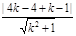=1.解得k=
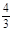或k=
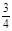.…………………………………8分
由l与P′Q关于y轴对称可得l的斜率为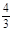－或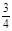－，…………………………10分
∴光线l所在的直线方程为y+1=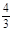－ (x－1)或y+1=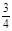－ (x－1),
即4x+3y－1=0或3x+4y+1=0. ………………………………12分
【解析】略
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
