题目内容
已知函数f(x)=ln(1+x)-ax的图象在x=1处的切线与直线x+2y-1=0平行.(Ⅰ)求实数a的值;
(Ⅱ)若方程f (x)=
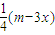 在[2,4]上有两个不相等的实数根,求实数m的取值范围;(参考数据:e=2.71 828…)
在[2,4]上有两个不相等的实数根,求实数m的取值范围;(参考数据:e=2.71 828…)(Ⅲ)设常数p≥1,数列{an}满足an+1=an+ln(p-an)(n∈N*),a1=lnp,求证:an+1≥an.
【答案】分析:(I)由函数f(x)=ln(1+x)-ax的图象在x=1处的切线与直线x+2y-1=0平行,则在x=1处的导数等于直线x+2y-1=0的斜率,从而求解.
(II)由(I)有f(x)=ln(1+x)-x,先将原方程整理为4ln(1+x)-x=m.再利用图象的交点来解决.(III)由f(x)=ln(1+x)-x(x>-1)用导数法证明当x∈(-1,+∞)时,f(x)≤0,得到ln(1+x)≤x.再由已知有p>an,构建an+1-an=ln(p-an)=ln(1+p-1-an)模型,只要再证11+p-1-an>1即可
解答:解:(I)∵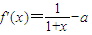 ,
,
∴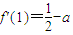 .
.
由题知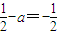 ,
,
解得a=1.(3分)
(II)由(I)有f(x)=ln(1+x)-x,
∴原方程可整理为4ln(1+x)-x=m.
令g(x)=4ln(1+x)-x,得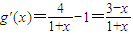 ,
,
∴当3<x≤4时g'(x)<0,当2≤x<3时g'(x)>0,g'(3)=0,
即g(x)在[2,3]上是增函数,在[3,4]上是减函数,
∴在x=3时g(x)有最大值4ln4-3.(6分)
∵g(2)=4ln3-2,g(4)=4ln5-4,
∴g(2)-g(4)=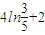 =2
=2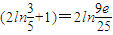 .
.
由9e≈24.46<25,于是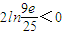 .
.
∴g(2)<g(4).
∴m的取值范围为[4ln5-4,4ln4-3).(9分)
(III)由f(x)=ln(1+x)-x(x>-1)有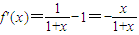 ,
,
显然f'(0)=0,当x∈(0,+∞)时,f'(x)<0,当x∈(-1,0)时,f'(x)>0,
∴f(x)在(-1,0)上是增函数,在[0,+∞)上是减函数.
∴f(x)在(-1,+∞)上有最大值f(0),而f(0)=0,
∴当x∈(-1,+∞)时,f(x)≤0,因此ln(1+x)≤x.(*)(11分)
由已知有p>an,即p-an>0,所以p-an-1>-1.
∵an+1-an=ln(p-an)=ln(1+p-1-an),
∴由(*)中结论可得an+1-an≤p-1-an,即an+1≤p-1(n∈N*).
∴当n≥2时,an+1-an=ln(p-an)≥ln[p-(p-1)]=0,即an+1≥an.
当n=1,a2=a1+ln(p-lnp),
∵lnp=ln(1+p-1)≤p-1,
∴a2≥a1+ln[p-(p-1)]=a1,结论成立.
∴对n∈N*,an+1≥an.(14分)
点评:本题主要考查导数的几何意义,用导数法解方程根的问题以及考查单调数列,综合性很强,要注意已证结论的应用.
(II)由(I)有f(x)=ln(1+x)-x,先将原方程整理为4ln(1+x)-x=m.再利用图象的交点来解决.(III)由f(x)=ln(1+x)-x(x>-1)用导数法证明当x∈(-1,+∞)时,f(x)≤0,得到ln(1+x)≤x.再由已知有p>an,构建an+1-an=ln(p-an)=ln(1+p-1-an)模型,只要再证11+p-1-an>1即可
解答:解:(I)∵
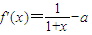 ,
,∴
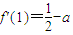 .
.由题知
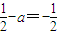 ,
,解得a=1.(3分)
(II)由(I)有f(x)=ln(1+x)-x,
∴原方程可整理为4ln(1+x)-x=m.
令g(x)=4ln(1+x)-x,得
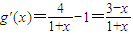 ,
,∴当3<x≤4时g'(x)<0,当2≤x<3时g'(x)>0,g'(3)=0,
即g(x)在[2,3]上是增函数,在[3,4]上是减函数,
∴在x=3时g(x)有最大值4ln4-3.(6分)
∵g(2)=4ln3-2,g(4)=4ln5-4,
∴g(2)-g(4)=
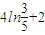 =2
=2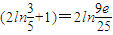 .
.由9e≈24.46<25,于是
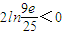 .
.∴g(2)<g(4).
∴m的取值范围为[4ln5-4,4ln4-3).(9分)
(III)由f(x)=ln(1+x)-x(x>-1)有
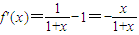 ,
,显然f'(0)=0,当x∈(0,+∞)时,f'(x)<0,当x∈(-1,0)时,f'(x)>0,
∴f(x)在(-1,0)上是增函数,在[0,+∞)上是减函数.
∴f(x)在(-1,+∞)上有最大值f(0),而f(0)=0,
∴当x∈(-1,+∞)时,f(x)≤0,因此ln(1+x)≤x.(*)(11分)
由已知有p>an,即p-an>0,所以p-an-1>-1.
∵an+1-an=ln(p-an)=ln(1+p-1-an),
∴由(*)中结论可得an+1-an≤p-1-an,即an+1≤p-1(n∈N*).
∴当n≥2时,an+1-an=ln(p-an)≥ln[p-(p-1)]=0,即an+1≥an.
当n=1,a2=a1+ln(p-lnp),
∵lnp=ln(1+p-1)≤p-1,
∴a2≥a1+ln[p-(p-1)]=a1,结论成立.
∴对n∈N*,an+1≥an.(14分)
点评:本题主要考查导数的几何意义,用导数法解方程根的问题以及考查单调数列,综合性很强,要注意已证结论的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目