题目内容
已知函数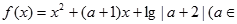 R,且
R,且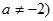
(I)若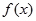 能表示成一个奇函数
能表示成一个奇函数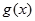 和一个偶函数
和一个偶函数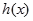 的和,求
的和,求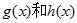 的解析式;
的解析式;
(II)命题P:函数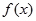 在区间
在区间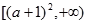 上是增函数;
上是增函数;
命题Q:函数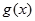 是减函数。
是减函数。
如果命题P、Q有且仅有一个是真命题,求a的取值范围;
(III)在(II)的条件下,比较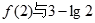 的大小。
的大小。
【答案】
(1)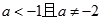 ;(2)
;(2)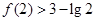
【解析】
试题分析:
(1)将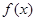 表示成奇函数
表示成奇函数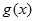 和一个偶函数
和一个偶函数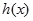 的和,分别求
的和,分别求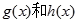 ,所用知识仅为函数的奇偶性,但是函数将三个函数
,所用知识仅为函数的奇偶性,但是函数将三个函数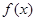 ,
,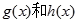 的奇偶性综合考察,出题者别具匠心,与以往单纯考察单个函数的奇偶性有较大区别。(2)函数
的奇偶性综合考察,出题者别具匠心,与以往单纯考察单个函数的奇偶性有较大区别。(2)函数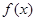 在区间
在区间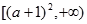 上是增函数,只需要二次函数对称轴≤
上是增函数,只需要二次函数对称轴≤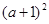 即可,
即可,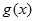 为一次函数,单调性只和系数相关,解答满足
为一次函数,单调性只和系数相关,解答满足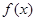 和
和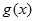 的参数范围,然后按照
的参数范围,然后按照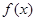 真、
真、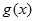 假和
假和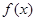 假、
假、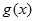 真求a的并集即可。(3)将
真求a的并集即可。(3)将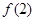 带入,看似与
带入,看似与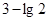 无关,但结合第二步结果
无关,但结合第二步结果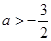 ,将a的值换成
,将a的值换成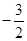 发现左右恰好相等,可以考虑右边定值,左边是函数在临界情况下的结果,研究左边表达式在
发现左右恰好相等,可以考虑右边定值,左边是函数在临界情况下的结果,研究左边表达式在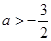 情况下的值域问题就可解决。
情况下的值域问题就可解决。
解答过程:(1)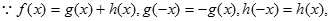
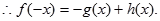
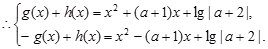
解得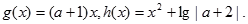 ……………………………………………4分
……………………………………………4分
(2)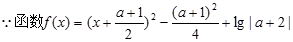 在区间
在区间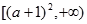 上是增函数,
上是增函数,
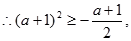 解得
解得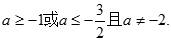
又由函数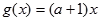 是减函数,得
是减函数,得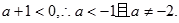
∴命题P为真的条件是: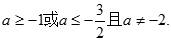
命题Q为真的条件是:
又∵命题P、Q有且仅有一个是真命题,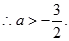 …………………………………8分
…………………………………8分
(2)由(1)得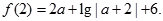
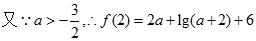
设函数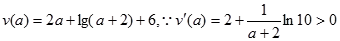
∴函数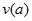 在区间
在区间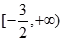 上为增函数
上为增函数
又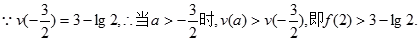 ………………12分
………………12分
考点:本题考查了函数奇偶性,含参二次函数和一次函数单调性,利用函数的导数求函数单调性以及逻辑问题。
点评:本题综合程度较高,考察内容灵活多变,除了第二步为常规思路解答。第一和第三步都值得认真去研究它的方法和解题思路,本题作为压轴题计算量不是很大,重要还是从本题中体现的方法值得深究。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 R,且
R,且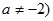
 能表示成一个奇函数
能表示成一个奇函数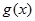 和一个偶函数
和一个偶函数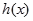 的和,求
的和,求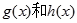 的解析式;
的解析式;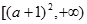 上是增函数;
上是增函数;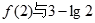 的大小。
的大小。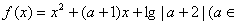 R,且
R,且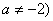 .
. 能表示成一个奇函数
能表示成一个奇函数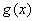 和一个偶函数
和一个偶函数 的和,求
的和,求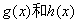 的解析式;
的解析式; 上是增函数;
上是增函数; 的大小.
的大小.