题目内容
已知函数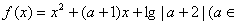 R,且
R,且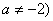 .
.
(I)若 能表示成一个奇函数
能表示成一个奇函数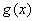 和一个偶函数
和一个偶函数 的和,求
的和,求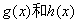 的解析式;
的解析式;
(II)命题P:函数 在区间
在区间 上是增函数;
上是增函数;
命题Q:函数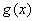 是减函数.
是减函数.
如果命题P、Q有且仅有一个是真命题,求a的取值范围;
(III)在(II)的条件下,比较 的大小.
的大小.
【答案】
解:(1)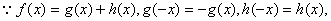
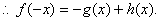
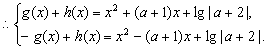
解得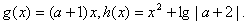
(2)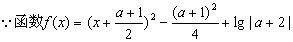 在区间
在区间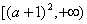 上是增函数,
上是增函数,
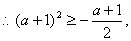 解得
解得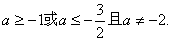
又由函数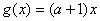 是减函数,得
是减函数,得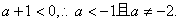
∴命题P为真的条件是: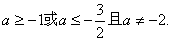
命题Q为真的条件是: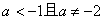 .
.
又∵命题P、Q有且仅有一个是真命题,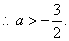
(2)由(1)得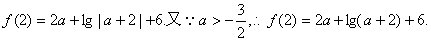
设函数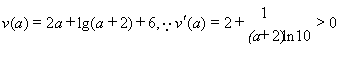 .
.
∴函数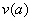 在区间
在区间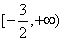 上为增函数.
上为增函数.
又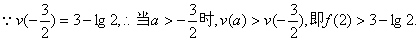

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 R,且
R,且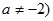
 能表示成一个奇函数
能表示成一个奇函数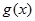 和一个偶函数
和一个偶函数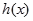 的和,求
的和,求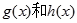 的解析式;
的解析式;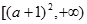 上是增函数;
上是增函数;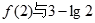 的大小。
的大小。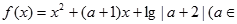 R,且
R,且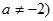
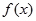 能表示成一个奇函数
能表示成一个奇函数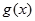 和一个偶函数
和一个偶函数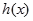 的和,求
的和,求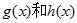 的解析式;
的解析式;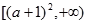 上是增函数;
上是增函数;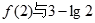 的大小。
的大小。