题目内容
【题目】如图,在同一个平面内,向量 ![]() ,
, ![]() ,
, ![]() 的模分别为1,1,
的模分别为1,1, ![]() ,
, ![]() 与
与 ![]() 的夹角为α,且tanα=7,
的夹角为α,且tanα=7, ![]() 与
与 ![]() 的夹角为45°.若
的夹角为45°.若 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),则m+n= .
(m,n∈R),则m+n= . 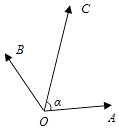
【答案】3
【解析】解:如图所示,建立直角坐标系.A(1,0).
由 ![]() 与
与 ![]() 的夹角为α,且tanα=7.
的夹角为α,且tanα=7.
∴cosα= ![]() ,sinα=
,sinα= ![]() .
.
∴C ![]() .
.
cos(α+45°)= ![]() (cosα﹣sinα)=
(cosα﹣sinα)= ![]() .
.
sin(α+45°)= ![]() (sinα+cosα)=
(sinα+cosα)= ![]() .
.
∴B ![]() .
.
∵ ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),
(m,n∈R),
∴ ![]() =m﹣
=m﹣ ![]() n,
n, ![]() =0+
=0+ ![]() n,
n,
解得n= ![]() ,m=
,m= ![]() .
.
则m+n=3.
故答案为:3.
如图所示,建立直角坐标系.A(1,0).由 ![]() 与
与 ![]() 的夹角为α,且tanα=7.可得cosα=
的夹角为α,且tanα=7.可得cosα= ![]() ,sinα=
,sinα= ![]() .C
.C ![]() .可得cos(α+45°)=
.可得cos(α+45°)= ![]() .sin(α+45°)=
.sin(α+45°)= ![]() .B
.B ![]() .利用
.利用 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),即可得出.
(m,n∈R),即可得出.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目