题目内容
(本小题满分14分)设 与
与 是函数
是函数 的两个极值点.
的两个极值点.
(1)试确定常数 和
和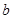 的值;
的值;
(2)试判断 是函数
是函数 的极大值点还是极小值点,并说明理由。
的极大值点还是极小值点,并说明理由。
 与
与 是函数
是函数 的两个极值点.
的两个极值点.(1)试确定常数
 和
和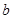 的值;
的值;(2)试判断
 是函数
是函数 的极大值点还是极小值点,并说明理由。
的极大值点还是极小值点,并说明理由。(1)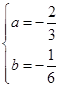 ;(2)当
;(2)当 是
是 的极小值点,当
的极小值点,当 是
是 的极大值点。
的极大值点。
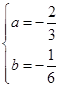 ;(2)当
;(2)当 是
是 的极小值点,当
的极小值点,当 是
是 的极大值点。
的极大值点。 根据函数在极值点处导数为0,得
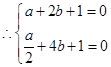 ,解之;
,解之;判断
 是函数
是函数 的极大值点还是极小值点,只需判断导数在
的极大值点还是极小值点,只需判断导数在 左右导数值的正负变化,由正至负极大值,由负至正极小值。
左右导数值的正负变化,由正至负极大值,由负至正极小值。解:(1)由题知
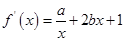 ┈┈┈┈┈┈┈┈┈┈┈┈2分
┈┈┈┈┈┈┈┈┈┈┈┈2分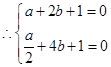 ┈┈┈┈┈┈┈┈┈┈┈┈2分
┈┈┈┈┈┈┈┈┈┈┈┈2分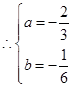 ┈┈┈┈┈┈┈┈┈┈┈┈2分
┈┈┈┈┈┈┈┈┈┈┈┈2分(2)由(1)知
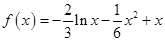 ┈┈┈┈┈┈┈┈┈┈┈┈1分
┈┈┈┈┈┈┈┈┈┈┈┈1分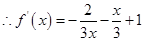 ┈┈┈┈┈┈┈┈┈┈┈┈1分
┈┈┈┈┈┈┈┈┈┈┈┈1分令
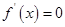 的
的 或
或 ┈┈┈┈┈┈┈┈┈┈┈┈1分
┈┈┈┈┈┈┈┈┈┈┈┈1分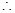 当
当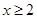 时
时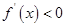 当
当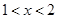 时
时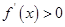
当
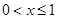 时
时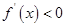 ┈┈┈┈┈┈┈┈┈┈┈┈3分
┈┈┈┈┈┈┈┈┈┈┈┈3分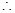 当
当 是
是 的极小值点, ┈┈┈┈┈┈┈┈┈┈┈┈1分
的极小值点, ┈┈┈┈┈┈┈┈┈┈┈┈1分当
 是
是 的极大值点。 ┈┈┈┈┈┈┈┈┈┈┈┈1分
的极大值点。 ┈┈┈┈┈┈┈┈┈┈┈┈1分
练习册系列答案
相关题目
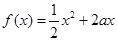 ,
,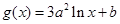 ,其中
,其中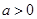 .
.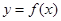 ,
,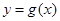 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.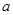 表示
表示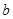 ;
;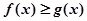 (
(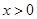 ).
). ,
, 为f(x)的导函数,令a=- ,b=log32,则下列关系正确的是( )
为f(x)的导函数,令a=- ,b=log32,则下列关系正确的是( )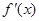 = 。
= 。 ,则
,则 ( )
( )








 的导数是( )
的导数是( )



 ,若
,若 ,则
,则 ( )
( )



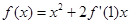 ,则
,则