题目内容
(满分14分)已知定义在正实数集上的函数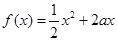 ,
,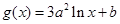 ,其中
,其中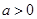 .
.
设两曲线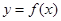 ,
,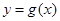 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(1)用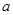 表示
表示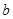 ;
;
(2)试证明不等式: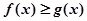 (
(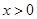 ).
).
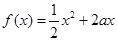 ,
,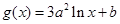 ,其中
,其中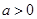 .
.设两曲线
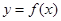 ,
,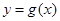 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.(1)用
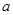 表示
表示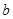 ;
;(2)试证明不等式:
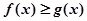 (
(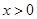 ).
).(1)  .
.
(2)见解析.
 .
.(2)见解析.
设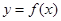 与
与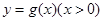 在公共点
在公共点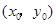 处的切线相同.所以
处的切线相同.所以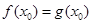 ,
, ,据此可建立关于a,b的关系式.
,据此可建立关于a,b的关系式.
(2)构造函数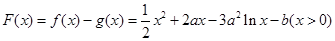 ,
,
然后研究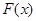 的最小值,证明最小值大于或等于零即可.
的最小值,证明最小值大于或等于零即可.
解:(1)设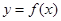 与
与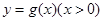 在公共点
在公共点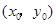 处的切线相同.……1分
处的切线相同.……1分
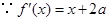 ,
,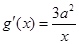 ,由题意
,由题意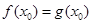 ,
, .……3分
.……3分
即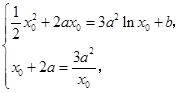 由
由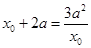 得:
得: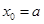 ,或
,或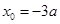 (舍去).……5分
(舍去).……5分
即有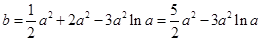 .……7分
.……7分
(2)设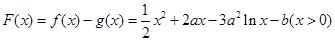 ,……8分
,……8分
则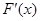
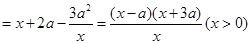 .……10分
.……10分
故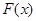 在
在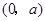 为减函数,在
为减函数,在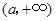 为增函数,……12分
为增函数,……12分
于是函数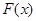 在
在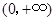 上的最小值是
上的最小值是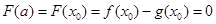 .……13分
.……13分
故当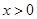 时,有
时,有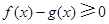 ,即当
,即当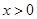 时,
时,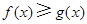 .……14分
.……14分
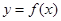 与
与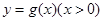 在公共点
在公共点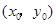 处的切线相同.所以
处的切线相同.所以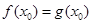 ,
, ,据此可建立关于a,b的关系式.
,据此可建立关于a,b的关系式.(2)构造函数
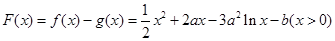 ,
,然后研究
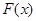 的最小值,证明最小值大于或等于零即可.
的最小值,证明最小值大于或等于零即可.解:(1)设
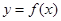 与
与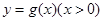 在公共点
在公共点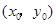 处的切线相同.……1分
处的切线相同.……1分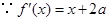 ,
,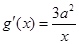 ,由题意
,由题意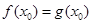 ,
, .……3分
.……3分即
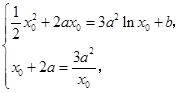 由
由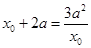 得:
得: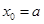 ,或
,或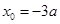 (舍去).……5分
(舍去).……5分即有
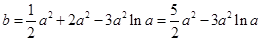 .……7分
.……7分(2)设
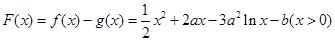 ,……8分
,……8分则
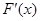
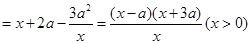 .……10分
.……10分故
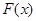 在
在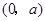 为减函数,在
为减函数,在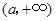 为增函数,……12分
为增函数,……12分于是函数
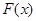 在
在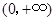 上的最小值是
上的最小值是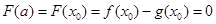 .……13分
.……13分故当
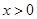 时,有
时,有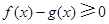 ,即当
,即当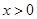 时,
时,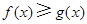 .……14分
.……14分
练习册系列答案
相关题目
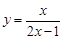 在点
在点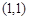 处的切线方程为 .
处的切线方程为 .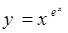 的导数,可先在两边取对数,得
的导数,可先在两边取对数,得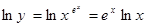 ,再在两边分别对x求导数,得
,再在两边分别对x求导数,得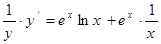 即为
即为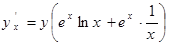 ,即导数为
,即导数为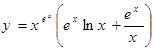 。若根据上面提供的方法计算函数
。若根据上面提供的方法计算函数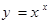 的导数,则
的导数,则 _
_  与
与 是函数
是函数 的两个极值点.
的两个极值点. 和
和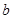 的值;
的值; 是函数
是函数 的极大值点还是极小值点,并说明理由。
的极大值点还是极小值点,并说明理由。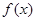 是定义在(0,
是定义在(0,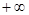 )上的非负可导函数,且满足
)上的非负可导函数,且满足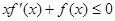 .对任意正数
.对任意正数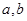 ,若
,若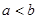 ,则必有( )
,则必有( )



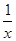 )′=1+
)′=1+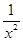

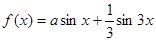 ,在
,在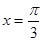 处有极值,则
处有极值,则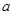 等于( )
等于( )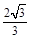
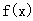 在
在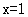 处的导数为3,则
处的导数为3,则



 在曲线
在曲线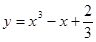 上移动时,过点
上移动时,过点