题目内容
某商品销售量 (件)与销售价格
(件)与销售价格 (元/件)负相关,则其回归方程可能是( )
(元/件)负相关,则其回归方程可能是( )
A. | B. |
C. | D. |
A
解析试题分析:因为商品销售量 (件)与销售价格
(件)与销售价格 (元/件)负相关,所以回归直线的斜率
(元/件)负相关,所以回归直线的斜率 ,排除
,排除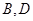 ,对于
,对于 选项,若价格定为
选项,若价格定为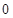 ,其销售量为
,其销售量为 ,显然不符合,所以回归方程可能为
,显然不符合,所以回归方程可能为 ,故选
,故选 .
.
考点:本题考查的知识点是回归分析的基本概念,重点考查了回归方程中回归系数与正负相关的关系,属于基础题.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案为了估计某水池中鱼的尾数,先从水池中捕出2000尾鱼,并给每尾鱼做上标记(不影响存活),然后放回水池,经过适当的时间,再从水池中捕出500尾鱼,其中有标记的鱼为40尾,根据上述数据估计该水池中鱼的尾数为( )
| A.10000 | B.20000 | C.25000 | D.30000 |
某调查机构调查了某地100个新生婴儿的体重,并根据所得数据画出了样本的频率分布直方图(如图所示),则新生婴儿的体重(单位:kg)在[3.2,4.0)的人数是( )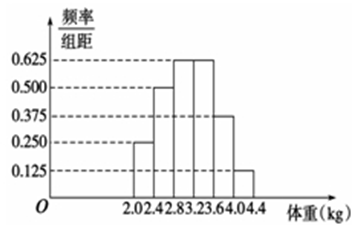
| A.30; | B.40; | C.50; | D.55. |
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 =0.85x-85.71,则下列结论中不正确的是( )
=0.85x-85.71,则下列结论中不正确的是( )
| A.y与x具有正的线性相关关系 |
B.回归直线过样本点的中心( , , ) ) |
| C.若该大学某女生身高增加1cm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重比为58.79kg |
某学校有体育特长生 人,美术特长生
人,美术特长生 人,音乐特长生
人,音乐特长生 人.用分层抽样的方法从中抽取
人.用分层抽样的方法从中抽取 人,则抽取的体育特长生、美术特长生、音乐特长生的人数分别为( )
人,则抽取的体育特长生、美术特长生、音乐特长生的人数分别为( )
A. 、 、 、 、 | B. 、 、 、 、 |
C. 、 、 、 、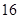 | D. 、 、 、 、 |
将参加夏令营的600名学生编号为:001,002,……600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495住在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为( )
| A.26,16,8, | B.25,17,8 | C.25,16,9 | D.24,17,9 |
在样本颇率分布直方图中,共有9个小长方形,若中间一个小长方形的面积等于它8个长方形的面积和的 ,且祥本容量为140,则中间一组的频数为( )
,且祥本容量为140,则中间一组的频数为( )
| A.28 | B.40 | C.56 | D.60 |
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.每组命中个数的茎叶图如下.则下面结论中错误的一个是( )
| A.甲的极差是29 |
| B.乙的众数是21 |
| C.甲罚球命中率比乙高 |
| D.甲的中位数是24 |
若回归直线方程的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( ).
A. =1.23x+4 =1.23x+4 | B. =1.23x+5 =1.23x+5 |
C. =1.23x+0.08 =1.23x+0.08 | D. =0.08x+1.23 =0.08x+1.23 |