题目内容
设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为
=0.85x-85.71，则下列结论中不正确的是( )
| A．y与x具有正的线性相关关系 |
B．回归直线过样本点的中心（ ， ） |
| C．若该大学某女生身高增加1cm，则其体重约增加0.85kg |
| D．若该大学某女生身高为170cm，则可断定其体重比为58.79kg |
D
解析试题分析：回归直线D散点图中点的分布从整体上看大致在一条直线附近,故A正确；回归直线一定过样本点的中心
但不一定过样本数据，故B正确；由回归直线方程可知
增加一个单位，体重就增加
，故C正确；回归直线对变量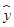
预测值，不可断定其体重为58.79kg，故D错误.
考点：考查线性回归方程，考查学生对线性回归方程的理解.
练习册系列答案
阅读快车系列答案
相关题目
一组数据的方差是s2，将这组数据中的每一个数据都乘以2，所得到的一组数据的方差是
| A．2s2 | B．4s2 | C．8s2 | D．16s2 |
某班有男生36人，女生18人，用分层抽样的方法从该班全体学生中抽取一个容量为9的样本，则抽取的女生人数为（ ）
| A．6 | B．4 | C．3 | D．2 |
四名同学根据各自的样本数据研究变量
之间的相关关系，并求得回归直线方程，
分别得到以下四个结论：
① y与x负相关且
；
② y与x负相关且
；
③ y与x正相关且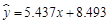
；
④ y与x正相关且
.
其中一定不正确的结论的序号是__________.
| A．①② | B．②③ | C．③④ | D．①④ |
某车间生产一种玩具,为了要确定加工玩具所需要的时间,进行了10次实验,数据如下:
| 玩具个数 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 加工时间 | 4 | 7 | 12 | 15 | 21 | 25 | 27 | 31 | 37 | 41 |
，则它的截距是 ( )A.
＝11－22； B.＝11－22； C.＝22－11； D.＝22－11. 某商品销售量
(件)与销售价格
(元/件)负相关,则其回归方程可能是( )
A． | B． |
C． | D． |
名工人某天生产同一零件，生产的件数是
设其平均数为
,中位数为
,众数为
，则有( )
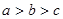
名高三学生期中考试数学成绩的频率分布直方图如图所示，由图中数据估计此次数学成绩平均分（ ）
