题目内容
10.(1)把参数方程$\left\{\begin{array}{l}{x={e}^{t}+{e}^{-t}}\\{y={e}^{t}-{e}^{-t}}\end{array}\right.$化为普通方程.(2)把极坐标方程4ρsin2$\frac{θ}{2}$=5化为直角坐标方程.
分析 (1)把参数方程中的x,y分别平方,然后作差,能求出普通方程.
(2)由sin2$\frac{θ}{2}$=$\frac{1-cosθ}{2}$,ρ2=x2+y2,ρcosθ=x,能把极坐标方程4ρsin2$\frac{θ}{2}$=5化为直角坐标方程.
解答 解:(1)∵$\left\{\begin{array}{l}{x={e}^{t}+{e}^{-t}}\\{y={e}^{t}-{e}^{-t}}\end{array}\right.$,∴$\left\{\begin{array}{l}{{x}^{2}={e}^{2t}+\frac{1}{{e}^{2t}}+2}\\{{y}^{2}={e}^{2t}+\frac{1}{{e}^{2t}}-2}\end{array}\right.$,x>0.
∴x2-y2=4,x>0
∴参数方程$\left\{\begin{array}{l}{x={e}^{t}+{e}^{-t}}\\{y={e}^{t}-{e}^{-t}}\end{array}\right.$的普通方程为x2-y2=4,(x>0).
(2)∵sin2$\frac{θ}{2}$=$\frac{1-cosθ}{2}$,
∴由4ρsin2$\frac{θ}{2}$=5,得2ρ(1-cosθ)=5,即2ρ-2ρcosθ=5,
由ρ2=x2+y2,ρcosθ=x,得2$\sqrt{{x}^{2}+{y}^{2}}$-2x=5,
化简得y2=5x+$\frac{25}{4}$,
∴把极坐标方程4ρsin2$\frac{θ}{2}$=5化为直角坐标方程得${y}^{2}=5x+\frac{25}{4}$.
点评 本题考查参数方程转化成普通方程,关键在于正确的消参.考查计算、分类讨论的意识和能力,解题时要注意二倍角公式的合理运用.

 全程金卷系列答案
全程金卷系列答案| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | .{1,2} | B. | {1} | C. | {-1,1} | D. | .∅ |
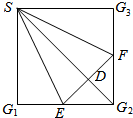 如图,在边长为a的正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个三棱锥,使G1,G2,G3三点重合,重合点记为G,则点G到平面SEF的距离为$\frac{a}{3}$.
如图,在边长为a的正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF及EF把这个正方形折成一个三棱锥,使G1,G2,G3三点重合,重合点记为G,则点G到平面SEF的距离为$\frac{a}{3}$.