题目内容
7.在边长为2的正方形ABCD中,E是边AB的中点,将△ADE沿DE折起使得平面ADE⊥平面BCDE,F是折叠后AC的中点.求二面角E-AB-D的平面角的余弦值.分析 以E为坐标原点,建立空间直角坐标系,分别求出平面EAB的法向量和平面ABD的法向量,由此能求出二面角E-AB-D的平面角的余弦值.
解答 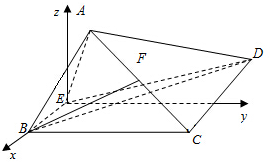 解:如图示以E为坐标原点,
解:如图示以E为坐标原点,
建立空间直角坐标系
则由已知得A$(-\frac{1}{5},\frac{2}{5},\frac{2}{{\sqrt{5}}})$,
B(1,0,0),D(-1,2,0)
设平面EAB的法向量为$\overrightarrow{n_1}=({x_1},{y_1},{z_1})$
则$\left\{\begin{array}{l}\overrightarrow{n_1}•\overrightarrow{EA}=0\\ \overrightarrow{n_1}•\overrightarrow{EB}=0\end{array}\right.⇒\left\{\begin{array}{l}-\frac{1}{5}{x_1}+\frac{2}{5}{y_1}+\frac{2}{{\sqrt{5}}}{z_1}=0\\{x_1}=0\end{array}\right.$
解得一个法向量为$\overrightarrow{n_1}=(0,\sqrt{5},-1)$,
设平面ABD的法向量为$\overrightarrow{n_2}=({x_2},{y_2},{z_2})$
则$\left\{\begin{array}{l}\overrightarrow{n_2}•\overrightarrow{BA}=0\\ \overrightarrow{n_2}•\overrightarrow{BD}=0\end{array}\right.⇒\left\{\begin{array}{l}-\frac{6}{5}{x_2}+\frac{2}{5}{y_2}+\frac{2}{{\sqrt{5}}}{z_2}=0\\-2{x_2}+2{y_2}=0\end{array}\right.$
解得一个法向量为$\overrightarrow{n_2}=(\sqrt{5},\sqrt{5},2)$,
∵$cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|{\overrightarrow{n_1}}|•|{\overrightarrow{n_2}}|}}=\frac{{\sqrt{21}}}{14}$,
∴二面角E-AB-D的平面角的余弦值$\frac{{\sqrt{21}}}{14}$.
点评 本题考查二面角的余弦值的求法,建立坐标系,利用向量法是解决空间二面角的常用方法.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案 执行如图所示的程序框图,若将判断框内“S>100”改为关于n的不等式“n≥n0”且要求输出的结果不变,则正整数n0的取值( )
执行如图所示的程序框图,若将判断框内“S>100”改为关于n的不等式“n≥n0”且要求输出的结果不变,则正整数n0的取值( )| A. | 是4 | B. | 是5 | C. | 是6 | D. | 不唯一 |
| A. | ($\frac{3}{2}$,4) | B. | ($\frac{3}{2}$,+∞) | C. | (4,+∞) | D. | (0,$\frac{3}{2}$) |
 如图,在正三棱柱ABC=A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M是棱CC1上一点.
如图,在正三棱柱ABC=A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M是棱CC1上一点.