题目内容
12.若抛物线y2=2px的焦点与双曲线$\frac{x^2}{6-k}+\frac{y^2}{2-k}$=1的右焦点重合,则p的值为( )| A. | 4 | B. | 2 | C. | -4 | D. | -2 |
分析 将双曲线化为标准方程,求出c值,得到焦点坐标,可得$\frac{p}{2}$=2,解得答案.
解答 解:∵双曲线$\frac{x^2}{6-k}+\frac{y^2}{2-k}$=1的标准方程为:$\frac{{x}^{2}}{6-k}-\frac{{y}^{2}}{k-2}$=1,
故c2=6-k+k-2=4,
故c=2,
即双曲线$\frac{x^2}{6-k}+\frac{y^2}{2-k}$=1的右焦点为(2,0),
故$\frac{p}{2}$=2,
解得:p=4,
故选:A
点评 本题考查抛物线,双曲线的定义、标准方程,以及简单性质的应用,熟练掌握抛物线的性质,是解答的关键.

练习册系列答案
相关题目
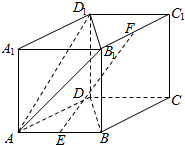 如图,在四棱柱 ABCD-A1 B1C1D1中,CC1⊥底面 ABCD,底面 ABCD为菱形,点 E,F分别是 AB,B1C1的中点,且∠DAB=60°,AA1=AB=2.
如图,在四棱柱 ABCD-A1 B1C1D1中,CC1⊥底面 ABCD,底面 ABCD为菱形,点 E,F分别是 AB,B1C1的中点,且∠DAB=60°,AA1=AB=2.