题目内容
设数列{xn}满足xn≠1且(n∈N*),前n项和为Sn.已知点p1(x1,S1),P2(x2,s2),…Pn(xn,sn)都在直线y=kx+b上(其中常数b,k且k≠1,b≠0),又yn=log
 .
.(1)求证:数列{xn]是等比数列;
(2)若yn=18-3n,求实数k,b的值;
(3)如果存在t、s∈N*,s≠t使得点(t,yt)和点(s,yt)都在直线y=2x+1上.问是否存在正整数M,当n>M时,xn>1恒成立?若存在,求出M的最小值,若不存在,请说明理由.
【答案】分析:(1)由an+1=Sn+1-Sn着手考虑,把点Pn、Pn+1的坐标代入直线y=kx+b,然后两式相减得xn+1与xn的关系式,即可得到结论;(2)由(1)知{xn}是等比数列,则根据条件消去yn得xn与n的关系式,此时与等比数列通项xn=x1qn-1相比较,易得x1与q,进而可求得k与b.
(3)由{xn}是等比数列且yn=log0.5xn可得数列{yn}为等差数列;当n>M时,xn>1恒成立问题应利用yn=log0.5xn转化为yn<0恒成立的问题,列不等式组,解出M,即可得到结论.
解答:(1)证明:∵点Pn(xn,Sn),Pn+1(xn+1,Sn+1)都在直线y=kx+b上,
∴Sn=kxn+b,Sn+1=kxn+1+b
两式相减得Sn+1-Sn=kxn+1-kxn,即xn+1=kxn+1-kxn,
∵常数k≠0,且k≠1,∴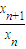 =
=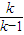 (非零常数)
(非零常数)
∴数列{xn]是等比数列;
(2)解:由yn=log0.5xn,得xn=( )yn=8n-6,
)yn=8n-6,
∴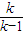 =8,得k=
=8,得k= .
.
又Pn在直线上,得Sn=kxn+b,
令n=1得b=S1- x1=-
x1=- x1=-
x1=-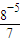 ;
;
(3)解:∵yn=log0.5xn,∴当n>M时,xn>1恒成立等价于yn<0恒成立.
∵存在t,s∈N*,使得(t,ys)和(s,yt)都在y=2x+1上,
∴ys=2t+1 ①,yt=2s+1 ②.
①-②得:ys-yt=2(t-s),
∵s≠t,∴{yn}是公差d=-2<0的等差数列
①+②得:ys+yt=2(t+s)+2,
又ys+yt=y1+(s-1)•(-2)+y1+(t-1)•(-2)=2y1-2(s+t)+4
由2y1-2(s+t)+4=2(t+s)+2,得y1=2(t+s)-1>0,
即:数列{yn}是首项为正,公差为负的等差数列,
所以一定存在一个最小自然数M,使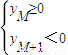 ,即
,即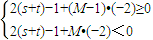
解得t+s- <M≤t+s+
<M≤t+s+ .
.
∵M∈N*,∴M=t+s.
即存在自然数M,其最小值为t+s,使得当n>M时,xn>1恒成立.
点评:本题考查等比数列的证明,考查等差数列,考查存在性问题,考查学生分析解决问题的能力,难度较大.
(3)由{xn}是等比数列且yn=log0.5xn可得数列{yn}为等差数列;当n>M时,xn>1恒成立问题应利用yn=log0.5xn转化为yn<0恒成立的问题,列不等式组,解出M,即可得到结论.
解答:(1)证明:∵点Pn(xn,Sn),Pn+1(xn+1,Sn+1)都在直线y=kx+b上,
∴Sn=kxn+b,Sn+1=kxn+1+b
两式相减得Sn+1-Sn=kxn+1-kxn,即xn+1=kxn+1-kxn,
∵常数k≠0,且k≠1,∴
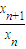 =
=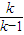 (非零常数)
(非零常数)∴数列{xn]是等比数列;
(2)解:由yn=log0.5xn,得xn=(
 )yn=8n-6,
)yn=8n-6,∴
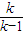 =8,得k=
=8,得k= .
.又Pn在直线上,得Sn=kxn+b,
令n=1得b=S1-
 x1=-
x1=- x1=-
x1=-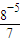 ;
;(3)解:∵yn=log0.5xn,∴当n>M时,xn>1恒成立等价于yn<0恒成立.
∵存在t,s∈N*,使得(t,ys)和(s,yt)都在y=2x+1上,
∴ys=2t+1 ①,yt=2s+1 ②.
①-②得:ys-yt=2(t-s),
∵s≠t,∴{yn}是公差d=-2<0的等差数列
①+②得:ys+yt=2(t+s)+2,
又ys+yt=y1+(s-1)•(-2)+y1+(t-1)•(-2)=2y1-2(s+t)+4
由2y1-2(s+t)+4=2(t+s)+2,得y1=2(t+s)-1>0,
即:数列{yn}是首项为正,公差为负的等差数列,
所以一定存在一个最小自然数M,使
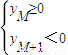 ,即
,即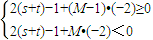
解得t+s-
 <M≤t+s+
<M≤t+s+ .
.∵M∈N*,∴M=t+s.
即存在自然数M,其最小值为t+s,使得当n>M时,xn>1恒成立.
点评:本题考查等比数列的证明,考查等差数列,考查存在性问题,考查学生分析解决问题的能力,难度较大.

练习册系列答案
相关题目
 .
. 没有实数根;
没有实数根; 的单调区间;
的单调区间; ,当a=2且
,当a=2且 ,证明:对任意m∈N*都有
,证明:对任意m∈N*都有 .
.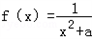 .
.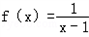 没有实数根;
没有实数根;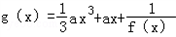 的单调区间;
的单调区间;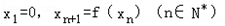 ,当a=2且
,当a=2且 ,证明:对任意m∈N*都有
,证明:对任意m∈N*都有 .
.