题目内容
设a>0,函数 .
.(1)求证:关于x的方程
 没有实数根;
没有实数根;(2)求函数
 的单调区间;
的单调区间;(3)设数列{xn}满足
 ,当a=2且
,当a=2且 ,证明:对任意m∈N*都有
,证明:对任意m∈N*都有 .
.
【答案】分析:(1)已知方程 ,可得
,可得 ,通分化简得到一元二次方程,用△来进行判断,方程有无解;
,通分化简得到一元二次方程,用△来进行判断,方程有无解;
(2)已知g(x)的解析式,根据求导法则求出g′(x),令g′(x)=0,先求出其极值点再研究其单调性,含有参量a,需要分类讨论;
(3)已知数列{xn}满足 ,将xm+k-xk=(xm+k-xm+k-1)+(xm+k-1-xm+k-2)+(xm+k-2-xm+k-3)…+(xk+1-xk),然后再进行放缩,求证;
,将xm+k-xk=(xm+k-xm+k-1)+(xm+k-1-xm+k-2)+(xm+k-2-xm+k-3)…+(xk+1-xk),然后再进行放缩,求证;
解答:解:(1)∵方程 ,∴
,∴ ,
,
∴x2-x+a+1=0,∵a>0,∴△=1-4(a+1)=-4a-3<0
方程 没有实数根;
没有实数根;
(2)∵函数 ,
,
∴g′(x)=ax2+2x+a,令g′(x)=ax2+2x+a=0,则△=4-4a2,
①当△=4-4a2,<0,即a>1,对任意实数g′(x)>0,
∴g(x)在R上单调递增
②当△=4-4a2,=0,即a=1,g′(1)=0,但g′(x)>0,(x≠1),
∴g(x)在R上单调递增
③当△=4-4a2,>0,即0<a<1,对任意实数由g′(x)>0,ax2+2x+a>0,得x 或x>
或x> ,
,
∴g(x)在( )上单调递减,
)上单调递减,
g(x)在(-∞, ),(
),( ,+∞)上单调递增
,+∞)上单调递增
(3)当a=2时,由x1=0,得 x2=f(x1)=f(0)= ,|x1-x2|=
,|x1-x2|= ,
,
|x1-x2|=| |=
|= ×|x22-x12|<
×|x22-x12|< ×|x2-x1||x2+x1|=
×|x2-x1||x2+x1|= ×
× ×|x2-x1|=
×|x2-x1|=
当k≥2时,∵0<xk≤
∴|xk+1-xk|=| |=
|= ×|xk2-xk-12|
×|xk2-xk-12| ×|xk-xk-1||xk+xk-1|<
×|xk-xk-1||xk+xk-1|< ×|xk-xk-1|
×|xk-xk-1|
< ×|xk-1-xk-2|<…<
×|xk-1-xk-2|<…< ×|x3-x2|<
×|x3-x2|<
对任意m∈N+,
|xm+k-xk|=|(xm+k-xm+k-1)+(xm+k-1-xm+k-2)+(xm+k-2-xm+k-3)…+(xk+1-xk)|≤|(xm+k-xm+k-1)|+|(xm+k-1-xm+k-2)|+••+|(xk+1-xk)|
≤( +
+ +…+
+…+ +1)|xk+1-xk|=
+1)|xk+1-xk|= |xk+1-xk|=
|xk+1-xk|= •
• =
= ,
,
即证;
点评:此题难度比较大,多次用到放缩,但是一、二问比较简单,利用导数来研究函f(x)的单调性和极值,第三问是数列综合题,关键是拆项找出规律,此题还利用了分类讨论的思想;
 ,可得
,可得 ,通分化简得到一元二次方程,用△来进行判断,方程有无解;
,通分化简得到一元二次方程,用△来进行判断,方程有无解;(2)已知g(x)的解析式,根据求导法则求出g′(x),令g′(x)=0,先求出其极值点再研究其单调性,含有参量a,需要分类讨论;
(3)已知数列{xn}满足
 ,将xm+k-xk=(xm+k-xm+k-1)+(xm+k-1-xm+k-2)+(xm+k-2-xm+k-3)…+(xk+1-xk),然后再进行放缩,求证;
,将xm+k-xk=(xm+k-xm+k-1)+(xm+k-1-xm+k-2)+(xm+k-2-xm+k-3)…+(xk+1-xk),然后再进行放缩,求证;解答:解:(1)∵方程
 ,∴
,∴ ,
,∴x2-x+a+1=0,∵a>0,∴△=1-4(a+1)=-4a-3<0
方程
 没有实数根;
没有实数根;(2)∵函数
 ,
,∴g′(x)=ax2+2x+a,令g′(x)=ax2+2x+a=0,则△=4-4a2,
①当△=4-4a2,<0,即a>1,对任意实数g′(x)>0,
∴g(x)在R上单调递增
②当△=4-4a2,=0,即a=1,g′(1)=0,但g′(x)>0,(x≠1),
∴g(x)在R上单调递增
③当△=4-4a2,>0,即0<a<1,对任意实数由g′(x)>0,ax2+2x+a>0,得x
 或x>
或x> ,
,∴g(x)在(
 )上单调递减,
)上单调递减,g(x)在(-∞,
 ),(
),( ,+∞)上单调递增
,+∞)上单调递增(3)当a=2时,由x1=0,得 x2=f(x1)=f(0)=
 ,|x1-x2|=
,|x1-x2|= ,
,|x1-x2|=|
 |=
|= ×|x22-x12|<
×|x22-x12|< ×|x2-x1||x2+x1|=
×|x2-x1||x2+x1|= ×
× ×|x2-x1|=
×|x2-x1|=
当k≥2时,∵0<xk≤

∴|xk+1-xk|=|
 |=
|= ×|xk2-xk-12|
×|xk2-xk-12| ×|xk-xk-1||xk+xk-1|<
×|xk-xk-1||xk+xk-1|< ×|xk-xk-1|
×|xk-xk-1|<
 ×|xk-1-xk-2|<…<
×|xk-1-xk-2|<…< ×|x3-x2|<
×|x3-x2|<
对任意m∈N+,
|xm+k-xk|=|(xm+k-xm+k-1)+(xm+k-1-xm+k-2)+(xm+k-2-xm+k-3)…+(xk+1-xk)|≤|(xm+k-xm+k-1)|+|(xm+k-1-xm+k-2)|+••+|(xk+1-xk)|
≤(
 +
+ +…+
+…+ +1)|xk+1-xk|=
+1)|xk+1-xk|= |xk+1-xk|=
|xk+1-xk|= •
• =
= ,
,即证;
点评:此题难度比较大,多次用到放缩,但是一、二问比较简单,利用导数来研究函f(x)的单调性和极值,第三问是数列综合题,关键是拆项找出规律,此题还利用了分类讨论的思想;

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
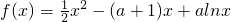 .
.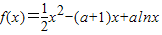 .
.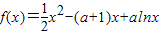 .
.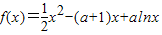 .
.