题目内容
已知 ,直线
,直线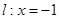 ,
,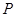 为平面上的动点,过点
为平面上的动点,过点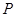 作
作 的垂线,垂足为点
的垂线,垂足为点 ,且
,且 .
.
(Ⅰ)求动点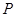 的轨迹曲线
的轨迹曲线 的方程;
的方程;
(Ⅱ)设动直线 与曲线
与曲线 相切于点
相切于点 ,且与直线
,且与直线 相交于点
相交于点 ,试问:在
,试问:在 轴上是否存在一个定点
轴上是否存在一个定点 ,使得以
,使得以 为直径的圆恒过此定点
为直径的圆恒过此定点 ?若存在,求出定点
?若存在,求出定点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(Ⅰ) (Ⅱ)存在一个定点
(Ⅱ)存在一个定点
 符合题意
符合题意
解析试题分析:(Ⅰ)设点 ,则
,则 ,由
,由 ,得
,得 ,化简得
,化简得 .
.
(Ⅱ)由 得
得 ,
,
由 ,得
,得 ,从而有
,从而有 ,
, ,
,
设点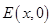 ,使得
,使得 ,则
,则
 得
得
所以存在一个定点
 符合题意
符合题意
考点:本小题主要考查相关点法求轨迹方程和直线与抛物线的位置关系的判断和应用.
点评:解决直线与圆锥曲线的位置关系问题时,一般离不开联立方程组,运算量较大,所以要仔细运算.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 =a,
=a, =b,求△ABC的面积.
=b,求△ABC的面积. 与
与 共线,设函数
共线,设函数 .
. 的周期及最大值;
的周期及最大值; ,边 BC=
,边 BC= ,
, ,求 △ABC 的面积.
,求 △ABC 的面积.
 的值;
的值; 且
且 ,求
,求 。
。 ,
, 。
。 及
及 ;
; 的最小值是
的最小值是 ,求
,求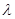 的值。
的值。
 与
与 平行,求实数
平行,求实数 的值.
的值.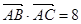 ,记
,记 ,△ABC的面积为
,△ABC的面积为 ,且满足
,且满足 .
. 的取值范围;
的取值范围; 的最大值和最小值.
的最大值和最小值. =
= ,
,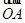 =
= ,
, =
=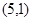 ,设
,设 是直线
是直线 上一点,
上一点, 是坐标原点
是坐标原点 取最小值时的
取最小值时的 ;
;  的余弦值。
的余弦值。 ,
, 与
与 夹角为
夹角为 ,求
,求 与
与 夹角的余弦值。
夹角的余弦值。