题目内容
6. 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=2AB=2,若E,F分别为线段A1D1,CC1的中点,则直线EF与平面ADD1A1所成角的正弦值为( )
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=2AB=2,若E,F分别为线段A1D1,CC1的中点,则直线EF与平面ADD1A1所成角的正弦值为( )| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{3}$ |
分析 取BB1中点为N,连接FN,取FN中点为M,连接A1M,A1F,易得∠MA1N为直线EF与平面ABB1A1所成角,解△MA1N即可求出直线EF与平面ABB1A1所成角的余弦值,进而可求正弦值.
解答 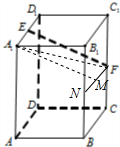 解:取BB1中点为N,连接FN,取FN中点为M,连接A1M,A1F 易得EF∥A1M,EF=A1M
解:取BB1中点为N,连接FN,取FN中点为M,连接A1M,A1F 易得EF∥A1M,EF=A1M
∵A1F是EF在面A1ABB1上的投影.
∴∠MA1N为所求的角.令AB=1,
在△MA1N中,A1N=$\sqrt{2}$,A1M=$\sqrt{3}$,
则cos∠MA1N=$\frac{\sqrt{6}}{3}$,所以sin∠MA1N=$\sqrt{1-\frac{6}{9}}$=$\frac{\sqrt{3}}{3}$.
故选C.
点评 本题考查的知识点是直线与平面所成的角,其中构造出线面夹角的平面角是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,椭圆C:x2+$\frac{{y}^{2}}{m}$=1(0<m<1)的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称.
如图所示,椭圆C:x2+$\frac{{y}^{2}}{m}$=1(0<m<1)的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称. 在如图所示的几何体中,四边形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3.
在如图所示的几何体中,四边形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3. 如图,在正三棱柱ABC-A1B1C1中(底面为正三角形且侧棱垂直于底面的三棱柱叫正三棱柱),各棱长都是4,D是BC的中点.
如图,在正三棱柱ABC-A1B1C1中(底面为正三角形且侧棱垂直于底面的三棱柱叫正三棱柱),各棱长都是4,D是BC的中点.