Question

已知函数f（x）=

x3(x＞0) (3-a)x-a(x≤0)

，给出下列四个命题：
（1）当a＞0时，函数f（x）的值域为[0，+∞），
（2）对于任意的x₁，x₂∈R，且x₁≠x₂，若

f(x1)-f(x2)

x1-x2

＞0恒成立，则a∈[0，3）；  
（3）对于任意的x₁，x₂∈（0，+∞），且x₁≠x₂，恒有

f(x1)+f(x)2

2

＜f（

x1+x2

2

）；  
（4）对于任意的x₁，x₂∈（0，+∞），且x₁≠x₂，若不等式|f（x₁）-f（x₂）|＞t|x₁-x₂|恒成立，则t的最大值为0．其中正确的有

（2）（4）

（只填相应的序号）

Answer 1

分析：对于（1）当特殊值a=3时，函数f（x）=

x3(x＞0) -3(x≤0)

，函数f（x）的值域为{3}∪[0，+∞）；（2）对于任意的x₁，x₂∈R，且x₁≠x₂，若

f(x1)-f(x2)

x1-x2

＞0恒成立，说明曲线上任意两点连线的斜率大于0，得出a的取值范围；对于（3）对于任意的x₁，x₂∈（0，+∞），且x₁≠x₂，由于三次函数的图象是下凸的；（4）对于任意的x₁，x₂∈（0，+∞），且x₁≠x₂，由三次函数的图象可知，对于其图象上任意两点的斜率的绝对值|

f(x 1)-f(x 2)

x 1-x2

|＞0，利用不等式t＜|

f(x 1)-f(x 2)

x 1-x2

|恒成立求得t的最大值．

解答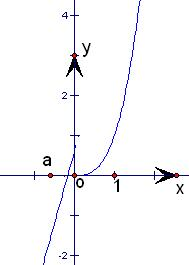：解：对于（1）当a=3时，函数f（x）=

x3(x＞0) -3(x≤0)

，函数f（x）的值域为{3}∪[0，+∞），故错；
（2）对于任意的x₁，x₂∈R，且x₁≠x₂，若

f(x1)-f(x2)

x1-x2

＞0恒成立，说明曲线上任意两点连线的斜率大于0，对于x≤0 时，射线y=（3-a）x-a的斜率3-a＞0，则a＜3，又当a＜0时，分段函数的图象如图所示，图象上有两点的连线的斜率小于0，不符合题意．故a∈[0，3）； 正确；
对于（3）对于任意的x₁，x₂∈（0，+∞），且x₁≠x₂，
由于三次函数的图象是下凸的，如图，利用梯形的中位线性质，得：

f(x1)+f(x2)

2

＞f（

x1+x2

2

）；故（3）不正确；
（4）对于任意的x₁，x₂∈（0，+∞），且x₁≠x₂，由三次函数的图象可知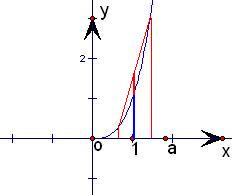，对于其图象上任意两点的斜率的绝对值|

f(x 1)-f(x 2)

x 1-x2

|＞0，不等式t＜|

f(x 1)-f(x 2)

x 1-x2

|恒成立，则t≤0，则若不等式|f（x₁）-f（x₂）|＞t|x₁-x₂|恒成立，则t的最大值为0．正确．
故答案为：（2）（4）．

点评：本小题主要考查函数单调性的性质、命题的真假判断与应用、函数的最值及其几何意义等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．