题目内容
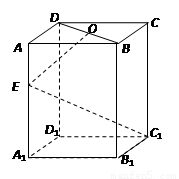
如图长方体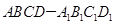 中,底面
中,底面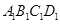 是正方形,
是正方形,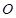 是
是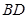 的中点,
的中点,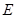 是棱
是棱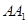 上任意一点.
上任意一点.
⑴求证: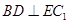 ;
;
⑵如果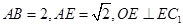 ,求
,求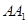 的长.
的长.
【答案】
(1)证明见解析;(2)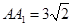 .
.
【解析】
试题分析:(1)要证线线垂直,一般可先证线面垂直,这个平面要包含其中一条直线,本题中有许多垂直关系,如 ,而
,而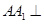 平面
平面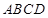
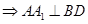 ,因此有
,因此有 平面
平面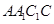 ,
, 正好是平面
正好是平面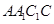 内的直线,问题得证;(2)我们采取空间问题平面化,所有条件都可在矩形
内的直线,问题得证;(2)我们采取空间问题平面化,所有条件都可在矩形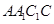 内,利用平面几何知识解题,由于
内,利用平面几何知识解题,由于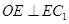 ,则有
,则有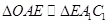 ,这两个三角形中,有
,这两个三角形中,有 ,又
,又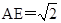 ,这时可求出
,这时可求出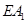 ,从而求出
,从而求出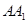 的长.
的长.
试题解析:(1)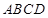 是正方形,∴
是正方形,∴ ,又长方体的侧棱
,又长方体的侧棱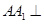 平面
平面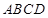 ,∴
,∴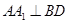 ,
,
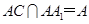 ,故有
,故有 平面
平面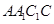 ,又
,又
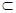
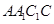 ,∴
,∴ . 7分
. 7分
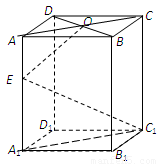
(2)在长方体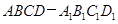 中,
中,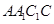 是矩形,由
是矩形,由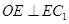 ,得
,得 ,∴
,∴ ,从而
,从而 ,∴
,∴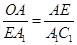 ,又底面正方形
,又底面正方形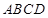 的边长为2,故
的边长为2,故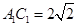 ,
,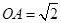 ,又
,又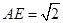 ,∴
,∴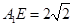 ,从而
,从而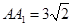 . 14分
. 14分
说明:用空间向量知识求解相应给分.
考点:(1)空间两直线垂直;(2)求线段长.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
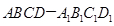 中,底面
中,底面 是正方形,
是正方形, 是
是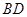 的中点,
的中点,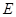 是棱
是棱 上任意一点.
上任意一点.
 ;
;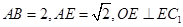 ,求
,求 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 为
为 与
与 的交点,
的交点, ,
,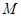 是线段
是线段 的中点.
的中点.
 平面
平面 ;
;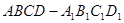 中,底面
中,底面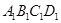 是正方形,
是正方形,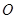 是
是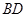 的中点,
的中点,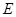 是棱
是棱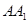 上任意一点。
上任意一点。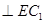 ;
;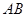 =2 ,
=2 ,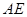 =
=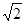 ,
,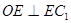 , 求
, 求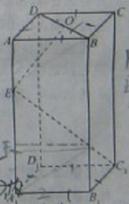
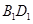
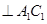 ,又侧棱垂直底面,可得
,又侧棱垂直底面,可得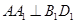 ,而
,而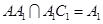 ,所以
,所以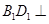 面
面 ,因
,因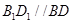 ,所以
,所以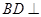 面
面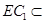 面
面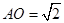 ,
,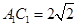 ,设
,设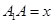 ,由
,由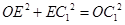 ,即
,即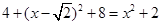 ,解得
,解得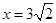 ,即
,即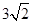 。
。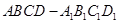 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形,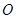 为
为 与
与 的交点,
的交点, ,
,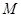 是线段
是线段 的中点.
的中点. 平面
平面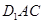 ;
; 平面
平面 ;
; 的大小.
的大小.