题目内容
设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,g(-2)=0且 >0,则 不等式g (x)
>0,则 不等式g (x) f(x) <0的解集是( )
f(x) <0的解集是( )
 >0,则 不等式g (x)
>0,则 不等式g (x) f(x) <0的解集是( )
f(x) <0的解集是( )| A.(-2, 0)∪(2,+ ∞) | B.(-2, 0)∪(0,2) |
| C.(-∞, -2)∪(2,+ ∞) | D.(-∞, -2)∪(0,2) |
D
令F(x)=f(x)g(x),因为f(x)、g(x)分别是定义在R上的奇函数和偶函数,所以F(x)为R上的奇函数,因为当x<0时, >0,所以F(x)在
>0,所以F(x)在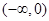 上是增函数,且F(-2)=0,所以F(x)在
上是增函数,且F(-2)=0,所以F(x)在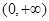 也是增函数,并且F(2)=0,所以F(x)<0的解集为(-∞, -2)∪(0,2).
也是增函数,并且F(2)=0,所以F(x)<0的解集为(-∞, -2)∪(0,2).
 >0,所以F(x)在
>0,所以F(x)在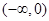 上是增函数,且F(-2)=0,所以F(x)在
上是增函数,且F(-2)=0,所以F(x)在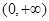 也是增函数,并且F(2)=0,所以F(x)<0的解集为(-∞, -2)∪(0,2).
也是增函数,并且F(2)=0,所以F(x)<0的解集为(-∞, -2)∪(0,2).
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
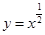 为导数的函数
为导数的函数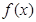 图象过点(9,1),则函数
图象过点(9,1),则函数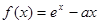 ,其中
,其中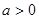 .
.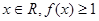 恒成立,求
恒成立,求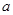 的取值范围;
的取值范围;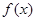 的图像上取定两点
的图像上取定两点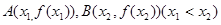 ,记直线
,记直线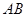 的斜率为
的斜率为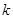 ,证明:存在
,证明:存在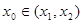 ,使
,使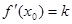 成立.
成立.
 .
. 为
为 的极值点,求实数
的极值点,求实数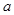 的值;
的值; 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值。
的最大值。 的图象在点P处的切线方程是
的图象在点P处的切线方程是 ,则
,则

 ,则
,则 的导函数
的导函数




 与
与 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若 ,则
,则


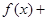
 在点
在点 处的导数是
处的导数是

 (
(
 且
且 ,则
,则 ( )
( )


