题目内容
已知不等式kx2-2x+6k<0的解集为B,A=(1,2),A⊆B,求实数k的取值范围.
分析:利用一元二次不等式的解集,利用A⊆B的关系确定k 的取值范围.
解答:解:①若k=0,则不等式等价为-2x<0,所以x>0,即B=(0,+∞).,
因为A=(1,2),所以A⊆B成立,所以此时k=0成立.
②若k≠0,设f(x)=kx2-2x+6k,设不等式的解为x1<x<x2,
则由题意可知x1≤1,x2≥2.
因为x1x2=6>0,所以对于方程的两个根同号.
所以要使A⊆B,则0<x1≤1,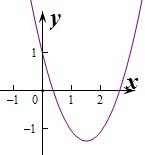
若k>0,则
,解得0<k≤
.
若k<0,f(x)=kx2-2x+6k的对称轴为x=-
=
<0,
此时函数f(x)在x>0时单调递减,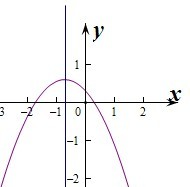
所以要使A⊆B,则有f(1)<0即可,即f(1)=k-2+6k=7k-2<0恒成立,
所以此时k<0.
综上满足条件的实数k的范围是k≤
.
因为A=(1,2),所以A⊆B成立,所以此时k=0成立.
②若k≠0,设f(x)=kx2-2x+6k,设不等式的解为x1<x<x2,
则由题意可知x1≤1,x2≥2.
因为x1x2=6>0,所以对于方程的两个根同号.
所以要使A⊆B,则0<x1≤1,

若k>0,则
|
| 2 |
| 7 |
若k<0,f(x)=kx2-2x+6k的对称轴为x=-
| -2 |
| 2k |
| 1 |
| k |
此时函数f(x)在x>0时单调递减,
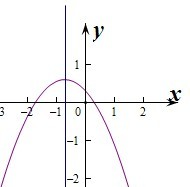
所以要使A⊆B,则有f(1)<0即可,即f(1)=k-2+6k=7k-2<0恒成立,
所以此时k<0.
综上满足条件的实数k的范围是k≤
| 2 |
| 7 |
点评:本题主要考查集合关系的应用,将不等式转化为函数,利用根的分布建立不等关系是解决本题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目