题目内容
已知负数a1和正数b1,且对任意的正整数n,当
≥0时,有[an+1,bn+1]=[an,
];当
<0时,有[an+1,bn+1]=[
,bn].
(1)求证数列{bn-an}是等比数列;
(2)若a1=-1,b1=2,求证a2n=-2b2n(n∈N*);
(3)是否存在a1,b1,使得数列{an}为常数数列?请说明理由.
| an+bn |
| 2 |
| an+bn |
| 2 |
| an+bn |
| 2 |
| an+bn |
| 2 |
(1)求证数列{bn-an}是等比数列;
(2)若a1=-1,b1=2,求证a2n=-2b2n(n∈N*);
(3)是否存在a1,b1,使得数列{an}为常数数列?请说明理由.
(1)当
≥0时,bn+1-an+1=
-an=
;
当
<0,bn+1-an+1=bn-
=
.
所以,总有bn+1-an+1=
(bn-an),
又b1>0,a1<0,可得b1-a1>0,
所以数列{bn-an}是等比数列.(4分)
(2)①由a1=-1,b1=2,可得
=
>0,
故有[a2,b2]=[a1,
],
∴b2=
=
,a2=a1=-1,从而a2=-2b2,
故当n=1时,a2n=-2b2n成立.(6分)
②假设当n=k时,a2n=-2b2n成立,即a2k=-2b2k,
由b2k-a2k=3b2k>0,可得b2k>0,
=
=-
<0,
故有[a2k+1,b2k+1]=[
,b2k],
∴a2k+1=
=-
,b2k+1=b2k,(9分)
=
=
>0,
故有[a2k+2,b2k+2]=[a2k+1,
]
∴b2k+2=
=
,a2k+2=a2k+1=-
,
故a2(k+1)=-2b2(k+1)
∴当n=k+1时,a2n=-2b2n成立.
综合①②可得对一切正整数n,都有a2n=-2b2n.(12分)
(3)假设存在a1,b1,使得数列{an}为常数数列,
由(1)可得bn-an=(b1-a1)(
)n-1,又an=a1,
故bn=a1+(b1-a1)(
)n-1,(14分)
由an+1=an恒成立,可知
≥0,即a1+(b1-a1)(
)n≥0恒成立,
即2n≤
对任意的正整数n恒成立,(16分)
又
是正数,
故n≤log2
对任意的正整数n恒成立,
因为log2
是常数,
故n≤log2
不可能对任意正整数n恒成立.
故不存在a1,b1,使得数列{an}为常数数列.(18分)
| an+bn |
| 2 |
| an+bn |
| 2 |
| bn-an |
| 2 |
当
| an+bn |
| 2 |
| an+bn |
| 2 |
| bn-an |
| 2 |
所以,总有bn+1-an+1=
| 1 |
| 2 |
又b1>0,a1<0,可得b1-a1>0,
所以数列{bn-an}是等比数列.(4分)
(2)①由a1=-1,b1=2,可得
| a1+b1 |
| 2 |
| 1 |
| 2 |
故有[a2,b2]=[a1,
| a1+b1 |
| 2 |
∴b2=
| a1+b1 |
| 2 |
| 1 |
| 2 |
故当n=1时,a2n=-2b2n成立.(6分)
②假设当n=k时,a2n=-2b2n成立,即a2k=-2b2k,
由b2k-a2k=3b2k>0,可得b2k>0,
| a2k+b2k |
| 2 |
| -2b2k+b2k |
| 2 |
| b2k |
| 2 |
故有[a2k+1,b2k+1]=[
| a2k+b2k |
| 2 |
∴a2k+1=
| a2k+b2k |
| 2 |
| b2k |
| 2 |
| a2k+1+b2k+1 |
| 2 |
-
| ||
| 2 |
| b2k |
| 4 |
故有[a2k+2,b2k+2]=[a2k+1,
| a2k+1+b2k+1 |
| 2 |
∴b2k+2=
| a2k+1+b2k+1 |
| 2 |
| b2k |
| 4 |
| b2k |
| 2 |
故a2(k+1)=-2b2(k+1)
∴当n=k+1时,a2n=-2b2n成立.
综合①②可得对一切正整数n,都有a2n=-2b2n.(12分)
(3)假设存在a1,b1,使得数列{an}为常数数列,
由(1)可得bn-an=(b1-a1)(
| 1 |
| 2 |
故bn=a1+(b1-a1)(
| 1 |
| 2 |
由an+1=an恒成立,可知
| an+bn |
| 2 |
| 1 |
| 2 |
即2n≤
| a1-b1 |
| a1 |
又
| a1-b1 |
| a1 |
故n≤log2
| a1-b1 |
| a1 |
因为log2
| a1-b1 |
| a1 |
故n≤log2
| a1-b1 |
| a1 |
故不存在a1,b1,使得数列{an}为常数数列.(18分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
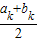 ≥0时,有ak+1=ak,bk+1=
≥0时,有ak+1=ak,bk+1=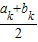 ;
;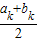 <0,有ak+1=
<0,有ak+1=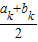 ,bk+1=bk.
,bk+1=bk.