题目内容
已知负数a和正数b,令a1=a,b1=b,且对任意的正整数k,当| ak+bk |
| 2 |
| ak+bk |
| 2 |
当
| ak+bk |
| 2 |
| ak+bk |
| 2 |
(1)求bn-an关于n的表达式;
(2)是否存在a,b,使得对任意的正整数n都有bn>bn+1?请说明理由.
(3)若对任意的正整数n,都有b2n-1>b2n,且b2n=b2n+1,求bn的表达式.
分析:(1)通过计算转化建立{bn-an}的相邻两项之间的关系是解决本题的关键,发现该数列是等比数列,从而确定出通项公式;
(2)首先假设存在合题意的a,b,然后确定出bn的关系式是解决本题的关键,通过分析其相邻项之间的关系达到解决该题的目的;
(3)通过bn的相应项之间的关系得到关于n的不等关系,利用加减项的方法确定出bn的表达式是解决本题的关键,注意对项数奇偶的讨论.
(2)首先假设存在合题意的a,b,然后确定出bn的关系式是解决本题的关键,通过分析其相邻项之间的关系达到解决该题的目的;
(3)通过bn的相应项之间的关系得到关于n的不等关系,利用加减项的方法确定出bn的表达式是解决本题的关键,注意对项数奇偶的讨论.
解答:解:(1)当
≥0时,bk+1-ak+1=
-ak=
;
当
<0,bk+1-ak+1=bk-
=
.
所以,总有bk+1-ak+1=
(bk-ak),
因此,数列{bn-an}是首项为b-a,公比为
的等比数列.
所以bn-an=(b-a)(
)n-1.
(2)假设存在a,b,对任意的正整数n都有bn>bn+1,即an=an+1.
所以an=an-1=…=a1=a,又bn-an=(b-a)(
)n-1,所以bn=a+(b-a)(
)n-1,
又
≥0,即a+(b-a)(
)n≥0,即2n≤
,
因为
是常数,故2n≤
不可能对任意正整数n恒成立.
故不存在a,b,使得对任意的正整数n都有bn>bn+1.
(3)由b 2n-1>b2n,可知a 2n-1=a2n,b2n=
,
所以b2n=
,即b2n-b 2n-1=-(b2n-a2n)=-(b-a)(
)2n-1.
又b2n=b 2n+1,故b 2n+1-b 2n-1=-(b2n-a2n)=-(b-a)(
)2n-1.
∴b 2n-1=(b 2n-1-b 2n-3)+(b 2n-3-b 2n-5)+…+(b3-b1)+b1
=(a-b)[(
)2n-3+(
)2n-5+…+(
)1]+b=
(a-b)[1-(
)n-1]+b.
当n为奇数时,令n=2m-1,可得bn=b 2m-1=
(a-b)[1-(
)m-1]+b=
(a-b)[1-(
)n-1]+b,
当n为偶数时,可得bn=b n+1=
(a-b)[1-(
)n]+b,
故bn=
.
| ak+bk |
| 2 |
| ak+bk |
| 2 |
| bk-ak |
| 2 |
当
| ak+bk |
| 2 |
| ak+bk |
| 2 |
| bk-ak |
| 2 |
所以,总有bk+1-ak+1=
| 1 |
| 2 |
因此,数列{bn-an}是首项为b-a,公比为
| 1 |
| 2 |
所以bn-an=(b-a)(
| 1 |
| 2 |
(2)假设存在a,b,对任意的正整数n都有bn>bn+1,即an=an+1.
所以an=an-1=…=a1=a,又bn-an=(b-a)(
| 1 |
| 2 |
| 1 |
| 2 |
又
| an+bn |
| 2 |
| 1 |
| 2 |
| a-b |
| a |
因为
| a-b |
| a |
| a-b |
| a |
故不存在a,b,使得对任意的正整数n都有bn>bn+1.
(3)由b 2n-1>b2n,可知a 2n-1=a2n,b2n=
| a2n-1+b2n-1 |
| 2 |
所以b2n=
| a2n+b2n-1 |
| 2 |
| 1 |
| 2 |
又b2n=b 2n+1,故b 2n+1-b 2n-1=-(b2n-a2n)=-(b-a)(
| 1 |
| 2 |
∴b 2n-1=(b 2n-1-b 2n-3)+(b 2n-3-b 2n-5)+…+(b3-b1)+b1
=(a-b)[(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
当n为奇数时,令n=2m-1,可得bn=b 2m-1=
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
当n为偶数时,可得bn=b n+1=
| 2 |
| 3 |
| 1 |
| 2 |
故bn=
|
点评:本题考查数列的综合问题,考查数列的递推关系与通项公式之间的关系,考查学生探究性问题的解决方法,注意体现转化与化归思想的运用,考查学生分析问题解决问题的能力和意识.

练习册系列答案
相关题目
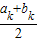 ≥0时,有ak+1=ak,bk+1=
≥0时,有ak+1=ak,bk+1=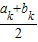 ;
;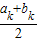 <0,有ak+1=
<0,有ak+1=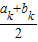 ,bk+1=bk.
,bk+1=bk.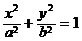 和
和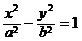 的离心率,则lge1+lge2的值为
的离心率,则lge1+lge2的值为