题目内容
(09年山东苍山期末文)(12分)
如下图所示:在直三棱柱ABC―A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点。

(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值。
解析:
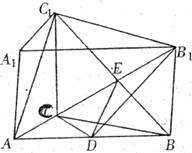
(1)直三棱角柱ABC―A1B1C1底面三边长AC=3,BC=4,AB=5
∴AC⊥BC且BC1在平面ABC内的射影为BC
∴AC⊥BC1
(2)设CB1与C1B的交点为E,连结DE
∵D是AB的中点,E是BC1的中点
∴DE∥AC1
DE![]() 平面CDB1,AC1
平面CDB1,AC1![]() 平面CDB1,
平面CDB1,
∴AC1平面CDB1
(3)DE∥AC1,∴∠CED为AC1与B1C所成的角
在△CED中,![]() ,
,![]() ,
,![]()
∴
∴异面直线AC1与B1C所成角的余弦值为![]() 。
。

练习册系列答案
相关题目
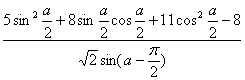 的值。
的值。