Question

将圆按向量a=（－1，2）平移后得到⊙O，直线l与⊙O相交于A、B两点，若在⊙O上存在点C，使 =λa，求直线l的方程及对应的点C的坐标．

Answer 1

直线l的方程为2x－4y＋5＝0，对应的C点的坐标为（－1，2）；或直线l的方程为2x－4y－5＝0，对应的C点的坐标为（1，－2）．

解析:

圆化为标准方程为，

按向量a＝（－1，2）平移得⊙O方程为 x²＋y²＝5．

∵＝λa，且||＝||，∴⊥，∥a．

∴k_AB＝．设直线l的方程为y＝x＋m，联立，得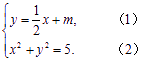

将方程（1）代入（2），整理得5x²＋4mx＋4m²－20＝0．（※）

设A（x₁，y₁），B（x₂，y₂），则

        x₁＋x₂＝－，y₁＋y₂＝，＝（－，）．

因为点C在圆上，所以，解之，得．

此时，（※）式中的△＝16m²－20(4m²－20)＝300＞0．

所求的直线l的方程为2x－4y＋5＝0，对应的C点的坐标为（－1，2）；或直线l的方程为2x－4y－5＝0，对应的C点的坐标为（1，－2）．