题目内容
已知复数z1=m+ni(m,n∈R),z=x+yi(x,y∈R),z2=2+4i且z=
i-z2.
(1)若复数z1对应的点M(m,n)在曲线y=-
(x+3)2-1上运动,求复数z所对应的点P(x,y)的轨迹方程;
(2)将(1)中的轨迹上每一点按向量
=(
,1)方向平移
个单位,得到新的轨迹C,求C的轨迹方程;
(3)过轨迹C上任意一点A(异于顶点)作其切线,交y轴于点B,求证:以线段AB为直径的圆恒过一定点,并求出此定点的坐标.
. |
| z1 |
(1)若复数z1对应的点M(m,n)在曲线y=-
| 1 |
| 2 |
(2)将(1)中的轨迹上每一点按向量
| a |
| 3 |
| 2 |
| ||
| 2 |
(3)过轨迹C上任意一点A(异于顶点)作其切线,交y轴于点B,求证:以线段AB为直径的圆恒过一定点,并求出此定点的坐标.
分析:(1)根据复数条件求出关系式
,结合复数z1对应的点M(m,n)在曲线y=-
(x+3)2-1上运动即可得出复数z所对应的点P(x,y)的轨迹方程;
(2)先按向量
=(
,1)方向平移
个单位得到即为向 x 方向移动 1×
=
个单位,向 y 方向移动 1×1=1 个单位,再进行函数式的变换即可得出C的轨迹方程;
(3)设A(x0,y0),斜率为k,切线y-y0=k(x-x0) 代入(y+6)2=-2x-3消去x得到关于y的一元二次方程,再结合根的判别式为0利用向量的数量即可求得定点,从而解决问题.
|
| 1 |
| 2 |
(2)先按向量
| a |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(3)设A(x0,y0),斜率为k,切线y-y0=k(x-x0) 代入(y+6)2=-2x-3消去x得到关于y的一元二次方程,再结合根的判别式为0利用向量的数量即可求得定点,从而解决问题.
解答:解:(1)∵
i-z2=(m-ni)•i-(2+4i)=(n-2)+(m-4)i;
∴
⇒
.
∵复数z1对应的点M(m,n)在曲线y=-
(x+3)2-1上运动
∴x+2=-
(y+7)2-1⇒(y+7)2=-2(x+3).
复数z所对应的点P(x,y)的轨迹方程:(y+7)2=-2(x+3).
(2)∵按向量
=(
,1)方向平移
个单位,
=
=1×
.
即为向 x 方向移动 1×
=
个单位,向 y 方向移动 1×1=1 个单位
(y+7)2=-2(x+3)⇒y+7=±
.
得轨迹方程 y+7=±
+1⇒(y+6)2=-2(x+
)=-2x-3.
C的轨迹方程为:(y+6)2=-2x-3.
(3)设A(x0,y0),斜率为k,切线y-y0=k(x-x0) (k≠0),
代入(y+6)2=-2x-3整理得:
(y+6)2=-2(
+x 0)-3,△=0⇒k=
,
设定点M(1,0),且
•
=0.
∴以线段AB为直径的圆恒过一定点M,M点的坐标(1,0).
. |
| z1 |
∴
|
|
∵复数z1对应的点M(m,n)在曲线y=-
| 1 |
| 2 |
∴x+2=-
| 1 |
| 2 |
复数z所对应的点P(x,y)的轨迹方程:(y+7)2=-2(x+3).
(2)∵按向量
| a |
| 3 |
| 2 |
| ||
| 2 |
(
|
| ||
| 2 |
| ||
| 2 |
即为向 x 方向移动 1×
| 3 |
| 2 |
| 3 |
| 2 |
(y+7)2=-2(x+3)⇒y+7=±
| -2(x+3) |
得轨迹方程 y+7=±
-2(x-
|
| 3 |
| 2 |
C的轨迹方程为:(y+6)2=-2x-3.
(3)设A(x0,y0),斜率为k,切线y-y0=k(x-x0) (k≠0),
代入(y+6)2=-2x-3整理得:
(y+6)2=-2(
| y-y 0 |
| k |
| x 0 |
| 2 |
设定点M(1,0),且
| AM |
| BM |
∴以线段AB为直径的圆恒过一定点M,M点的坐标(1,0).
点评:本小题主要考查抛物线的简单性质、直线与圆的位置关系等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,本题巧妙地把点的轨迹方程和复数有机地结合在一起,解题时要注意复数的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
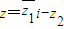 .
.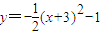 上运动,求复数z所对应的点P(x,y)的轨迹方程;
上运动,求复数z所对应的点P(x,y)的轨迹方程;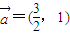 方向平移
方向平移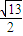 个单位,得到新的轨迹C,求C的轨迹方程;
个单位,得到新的轨迹C,求C的轨迹方程;