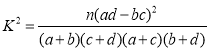题目内容
【题目】在直角坐标系
中，以坐标原点为极点，
轴正半轴为极轴建立极坐标系，曲线
的极坐标方程是
，曲线
的参数方程为：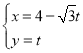
（
为参数）.
（1）求曲线，的直角坐标方程；
（2）设曲线，交于点
，
，已知点
，求
.
【答案】（1）曲线
的直角坐标方程为：
，曲线
的直角坐标方程为：
（2）
【解析】
（1）根据极坐标和直角坐标、参数方程的互化公式得结果；
（2）将直线的参数方程代入曲线的直角坐标方程，整理可得t2-(4
t+16＝0，利用参数的几何意义及韦达定理可得结论；
（1）曲线的极坐标方程可以化为：
，
所以曲线的直角坐标方程为：，
曲线的直角坐标方程为：.
（2）曲线的参数方程可化为：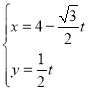
（
为参数），
将的参数方程代入曲线的直角坐标方程得到：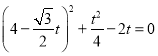
，
整理得：
，判别式
，
不妨设
，
的参数分别为
，
，则
，
，
又点
，所以
，
，所以
，
又因为
，
，所以
，
，
.
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
