题目内容
21.已知椭圆
21.本小题主要考查椭圆和直线的基础知识以及综合运用知识解决问题的能力.
证明一:依题设,得椭圆的半焦距c=1,右焦点为F(1,0),右准线方程为x=2,点E的坐标为(2,0),EF的中点为N(![]() ,0).
,0).
若AB垂直于x轴,则A(1,y1),B(1,-y1),C(2,-y1),
所以AC中点为N(![]() ,0),即AC过EF中点N.
,0),即AC过EF中点N.
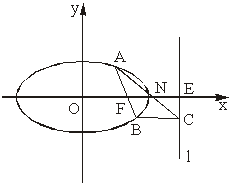
若AB不垂直于x轴,由直线AB过点F,且由BC∥x轴知点B不在x轴上,故直线AB的方程为
y=k(x-1),k≠0.记A(x1,y1)和B(x2,y2),则C(2,y2)且x1,x2满足二次方程![]() +k2(x-1)2=1,
+k2(x-1)2=1,
即 (1+2k2)x2-4k2x+2(k2-1)=0,
所以 x1+ x2=![]() , x1x2=
, x1x2=![]() .
.
又x12=2-2y12<2,得x1-![]() ≠0,故直线AN,CN的斜率分别为
≠0,故直线AN,CN的斜率分别为
k1=![]() =
=![]() ,
,
k2=![]() =2k(x2-1).
=2k(x2-1).
所以 k1-k2=2k·![]()
因为 (x1-1)-(x2-1)(2x1-3)
=3(x1+x2)-2x1x2-4
=![]() [12k2-4(k2-1)-4(1+2k2)]
[12k2-4(k2-1)-4(1+2k2)]
=0,
所以k1-k2=0,即k1=k2,故A、C、N三点共线.
所以,直线AC经过线段EF的中点N.
证明二:如图,记直线AC与x轴的交点为N,过A作AD⊥l,D是垂足.因为F是椭圆的右焦点,l是右准线,
BC∥x轴,即BC⊥l,根据椭圆几何性质,得:![]() =
=![]() =e (e是椭圆的离心率),
=e (e是椭圆的离心率),
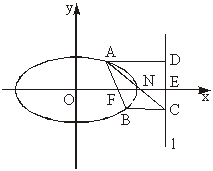
因为AD∥FE∥BC,
所以![]() =
=![]() =
=![]() ,
,![]() =
=![]() ,
,
即得|EN|=![]() = e·
= e·![]() =
=![]() =|FN|,
=|FN|,
所以N为EF的中点,即直线AC经过线段EF的中点N.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 +y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.
+y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.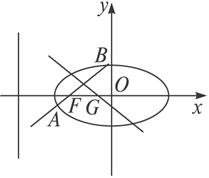
 +y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.
+y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.