题目内容
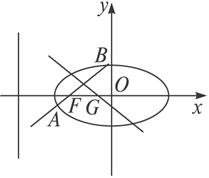
已知椭圆 +y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.
+y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.( I ) 求三棱锥A-F1F2B的体积;
(Ⅱ)图2中线段BF2上是否存在点M,使得AM⊥OB,若存在,请在图1中指出点M的坐标;若不存在,请说明理由.
【答案】分析:(Ⅰ)利用椭圆的标准方程及其性质、面面垂直的性质及三棱锥的体积计算公式即可得出;
(Ⅱ)利用线线垂直的斜率之间的关系、线面垂直的判定和性质定理即可得出.
解答:解:(Ⅰ)由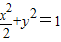 得a2=2,b2=1,∴b=1,
得a2=2,b2=1,∴b=1,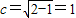 .
.
∴上顶点A(0,1),左焦点F1(-1,0),右焦点F2(1,0).
直线AF1:y=x+1,联立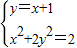 消去y点得到3x2+4x=0,
消去y点得到3x2+4x=0,
解得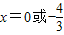 ,
,
∴B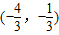 .
.
∴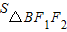 =
=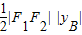 =
=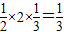 .
.
∵平面AF1F2⊥平面BF1F2,平面AF1F2∩平面BF1F2=F1F2,AO⊥F1F2,
∴AO⊥平面BF1F2.
∴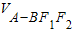 =
=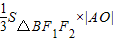 =
=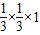 =
= .
.
(Ⅱ)假设存在点M,使得AM⊥OB,由(Ⅰ)可知AO⊥平面BF1F2,∴AO⊥BO.
过点O作OM⊥OB交BF2于点M,连接AM.
∵kOB=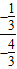 =
= ,∴kOM=-4,∴直线OM的方程为y=-4x.
,∴kOM=-4,∴直线OM的方程为y=-4x.
直线BF2的方程为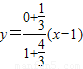 ,化为
,化为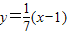 .
.
联立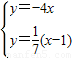 ,解得
,解得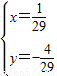 ,
,
∴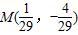 ,可知点M在线段BF2上,
,可知点M在线段BF2上,
由以上作法可知:BO⊥平面AOM,∴BO⊥AM,满足条件.
因此图2中线段BF2上存在点M,使得AM⊥OB,图1中点M的坐标为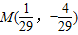 .
.
点评:是掌握椭圆的标准方程及其性质、线面与面面垂直的判定和性质定理及三棱锥的体积计算公式、线线垂直的斜率之间的关系是解题的关键.
(Ⅱ)利用线线垂直的斜率之间的关系、线面垂直的判定和性质定理即可得出.
解答:解:(Ⅰ)由
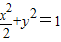 得a2=2,b2=1,∴b=1,
得a2=2,b2=1,∴b=1,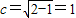 .
.∴上顶点A(0,1),左焦点F1(-1,0),右焦点F2(1,0).
直线AF1:y=x+1,联立
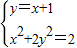 消去y点得到3x2+4x=0,
消去y点得到3x2+4x=0,解得
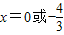 ,
,∴B
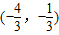 .
.∴
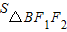 =
=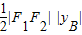 =
=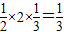 .
.∵平面AF1F2⊥平面BF1F2,平面AF1F2∩平面BF1F2=F1F2,AO⊥F1F2,

∴AO⊥平面BF1F2.
∴
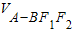 =
=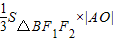 =
=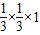 =
= .
.(Ⅱ)假设存在点M,使得AM⊥OB,由(Ⅰ)可知AO⊥平面BF1F2,∴AO⊥BO.
过点O作OM⊥OB交BF2于点M,连接AM.
∵kOB=
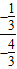 =
= ,∴kOM=-4,∴直线OM的方程为y=-4x.
,∴kOM=-4,∴直线OM的方程为y=-4x.直线BF2的方程为
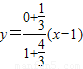 ,化为
,化为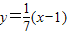 .
.联立
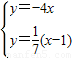 ,解得
,解得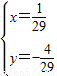 ,
,∴
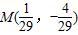 ,可知点M在线段BF2上,
,可知点M在线段BF2上,由以上作法可知:BO⊥平面AOM,∴BO⊥AM,满足条件.
因此图2中线段BF2上存在点M,使得AM⊥OB,图1中点M的坐标为
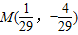 .
.点评:是掌握椭圆的标准方程及其性质、线面与面面垂直的判定和性质定理及三棱锥的体积计算公式、线线垂直的斜率之间的关系是解题的关键.

练习册系列答案
相关题目
 +y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.
+y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.