题目内容
3.已知椭圆的中心在原点,离心率为$\frac{1}{2}$,一个焦点是F(-1,0).(1)求椭圆的标准方程;
(2)设Q是椭圆上的一点,过点F、Q的直线l与y轴交于点M,且$\overrightarrow{MQ}$=2$\overrightarrow{QF}$,求直线l的斜率.
分析 (1)由题意的离心率公式和a,b,c的关系,可得a,b,进而得到椭圆方程;
(2)设Q(x0,y0),F(-1,0),设l:y=k(x+1),M(0,k),运用向量共线的坐标表示,求得Q的坐标,代入椭圆方程,计算即可得到k的值.
解答 解:(1)由题意:$c=1,\frac{c}{a}=\frac{1}{2}⇒a=2,b=\sqrt{3}$,
所以椭圆方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(2)设Q(x0,y0),F(-1,0),
设l:y=k(x+1),M(0,k),
因为$\overrightarrow{MQ}$=2$\overrightarrow{QF}$,即有(x0,y0-k)=2(-1-x0,-y0),
得$\left\{\begin{array}{l}{x_0}=-\frac{2}{3}\\{y_0}=\frac{k}{3}\end{array}\right.$,所以$Q(-\frac{2}{3},\frac{k}{3})$,
代入椭圆方程可得,$\frac{{\frac{4}{9}}}{4}+\frac{{\frac{k^2}{9}}}{3}=1⇒{k^2}=24⇒k=±2\sqrt{6}$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式,同时考查直线的斜率的求法,注意直线方程和向量共线的坐标表示,考查运算能力,属于中档题.

练习册系列答案
相关题目
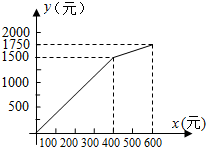 某游艺场每天的盈利额y元与售出的门票数x张之间的关系如图所示,试问盈利额为750元时,当天售出的门票数为多少?
某游艺场每天的盈利额y元与售出的门票数x张之间的关系如图所示,试问盈利额为750元时,当天售出的门票数为多少?