题目内容
平面直角坐标系中,动点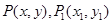 ,向量
,向量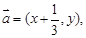
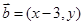
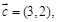
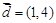 ,且
,且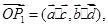 若
若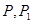 在同一条直线上运动,则这样的直线
在同一条直线上运动,则这样的直线
A.不存在 B.存在无数条 C.存在两条 D.存在一条
【答案】
D
【解析】
试题分析:因为向量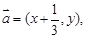

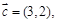
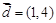 ,
,
所以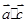 =3x+1+2y,
=3x+1+2y,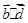 =x-3+4y,
=x-3+4y,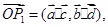 =(3x+2y+1,x+4y-3),
=(3x+2y+1,x+4y-3),
又因为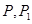 在同一条直线上运动,所以存在实数t,使
在同一条直线上运动,所以存在实数t,使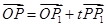 ,
,
即(x,y)=(3x+2y+1,x+4y-3)+t(2x+2y+1,x+3y-3), t(2x+2y+1)=-2x-2y-1且t(x+3y-3)=-x-3y+3,
所以t=-1,这样的直线存在一条,选D。
考点:本题主要考查平面向量的坐标运算,直线的参数式方程。
点评:中档题,平面向量是高考必考内容,其中数量积、坐标运算是重点。本题经过逐步计算,确定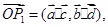 后,利用
后,利用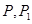 在同一条直线上运动,确定参数,判断出直线条数。
在同一条直线上运动,确定参数,判断出直线条数。

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
在平面直角坐标系中,动点M(x,y)满足条件
,动点Q在曲线(x-1)2+y2=
上,则|MQ|的最小值为( )
|
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、1-
| ||||
D、
|