题目内容
甲,乙两人射击,每次射击击中目标的概率分别是| 1 |
| 3 |
| 1 |
| 4 |
(Ⅰ)求3次射击的人依次是甲、甲、乙的概率;
(Ⅱ)若射击击中目标一次得1分,否则得0分(含未射击).用ξ表示乙的总得分,求ξ的分布列和数学期望.
分析:(Ⅰ)3次射击的人依次是甲、甲、乙,它所包含的事件是甲第一次击中,接着射击第二次,但是第二次没有击中,根据每人每次射击击中目标与否均互不影响.得到本题是一个相互独立事件同时发生的概率.
(Ⅱ)甲、乙两人共射击3次,且第一次由甲开始射击,可由题意知ξ的可能取值为0,1,2,结合变量对应的事件,写出三种情况的概率,写出分布列和期望.
(Ⅱ)甲、乙两人共射击3次,且第一次由甲开始射击,可由题意知ξ的可能取值为0,1,2,结合变量对应的事件,写出三种情况的概率,写出分布列和期望.
解答:解:(Ⅰ)3次射击的人依次是甲、甲、乙,
它所包含的事件是甲第一次击中,接着射击第二次,但是第二次没有击中,
记“3次射击的人依次是甲、甲、乙”为事件A.
每人每次射击击中目标与否均互不影响.
由题意得事件A的概率P(A)=
×
=
;
(Ⅱ)由题意,ξ的可能取值为0,1,2,
P(ξ=0)=
×
+
×
×
+
×
=
;
P(ξ=1)=
×
×
+
×
×
=
;
P(ξ=2)=
×
×
=
.
∴ξ的分布列为:
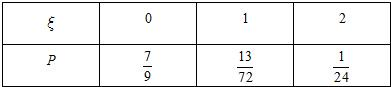
∴ξ的数学期望Eξ=0×
+1×
+2×
=
.
它所包含的事件是甲第一次击中,接着射击第二次,但是第二次没有击中,
记“3次射击的人依次是甲、甲、乙”为事件A.
每人每次射击击中目标与否均互不影响.
由题意得事件A的概率P(A)=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
(Ⅱ)由题意,ξ的可能取值为0,1,2,
P(ξ=0)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| 7 |
| 9 |
P(ξ=1)=
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 13 |
| 72 |
P(ξ=2)=
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 24 |
∴ξ的分布列为:

∴ξ的数学期望Eξ=0×
| 7 |
| 9 |
| 13 |
| 72 |
| 1 |
| 24 |
| 19 |
| 72 |
点评:本题考查相互独立事件同时发生的概率,离散型随机变量的分布列和期望,考查运用概率知识解决实际问题的能力,相互独立事件是指,两事件发生的概率互不影响,注意应用相互独立事件同时发生的概率公式.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目