题目内容
已知圆x2+y2=8,定点P(4,0),问过点P的直线的倾斜角在什么范围内取值时,该直线与已知圆无公共点.
【答案】分析:通过直线的斜率存在与不存在两种情况,分别解答,利用直线与已知圆无公共点,就是圆心到直线的距离大于半径,求出斜率的范围.
解答:解:①当直线的斜率不存在时,即直线的倾斜角为90°,
因为圆x2+y2=8的圆心(0,0),半径是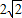 ,
,
所以直线方程是x=4与圆x2+y2=8无公共点.
②当直线的斜率存在时,设直线的斜率为k,则直线方程为:y=k(x-4),即kx-y-4k=0.
由直线与圆无公共点,
所以圆心到直线的距离公式得: ,
,
求得k>1或k<-1
所以,倾斜角为(45°,90°)∪(90°,135°)
综上,倾斜角的范围为(45°,135°).
点评:本题是中档题,考查直线与圆的位置关系,考查分类讨论思想,转化思想与计算能力.
解答:解:①当直线的斜率不存在时,即直线的倾斜角为90°,
因为圆x2+y2=8的圆心(0,0),半径是
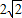 ,
,所以直线方程是x=4与圆x2+y2=8无公共点.
②当直线的斜率存在时,设直线的斜率为k,则直线方程为:y=k(x-4),即kx-y-4k=0.
由直线与圆无公共点,
所以圆心到直线的距离公式得:
 ,
,求得k>1或k<-1
所以,倾斜角为(45°,90°)∪(90°,135°)
综上,倾斜角的范围为(45°,135°).
点评:本题是中档题,考查直线与圆的位置关系,考查分类讨论思想,转化思想与计算能力.

练习册系列答案
相关题目