Question

已知圆x²+y²=8，定点P(4，0)，问过P点的直线的斜率在什么范围内取值时，这条直线与已知圆：(1)相切，(2)相交，(3)相离，并写出过P点的切线方程.

Answer 1

解析：解法一  设过P点的直线的斜率为k(由已知k存在)，则其方程为y=k(x-4)

由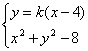  消去y，得x²+k²(x-4)²=8，

即(1+k²)x²-8k²x+16k²-8=0,

Δ=(-8k²)²-4(1+k²)(16k²-8)=32(1-k²).

(1)令Δ=0，即      32(1-k²)=0,

∴ 当k=±1时，直线与圆相切，切线方程为

x-y-4=0或x+y-4=0.

(2)令Δ＞0，即32(1-k²)＞0,-1＜k＜1,

∴ 当-1＜k＜1时，直线与圆相交.

(3)令Δ＜0，即32(1-k²)＜0,k＞1或k＜-1,

∴ 当k＜-1或k＞1时，直线与圆相离.

解法二：设圆心到直线的距离为d，则

(1)d=r，即，∴k²=1，∴k=±1时直线与圆相切，其切线方程为    x-y-4=0或x+y-4=0.

(2)d＜r，即，∴ k²＜1，即-1＜k＜1时直线与圆相交.

(3)d＞r，即， ∴ k²＞1，即k＜-1或k＞1时直线与圆相离.