题目内容
已知圆x2+y2=8内一点P0(-1,2),AB为过点P0且倾斜角为α的弦.
(1)当α=135°时,求AB的长.
(2)当 弦AB最长时,求出直线AB的方程.
(3)当弦AB被点P0平分时,求出直线AB的方程.
(1)当α=135°时,求AB的长.
(2)当 弦AB最长时,求出直线AB的方程.
(3)当弦AB被点P0平分时,求出直线AB的方程.
分析:(1)根据直线的倾斜角算出直线的斜率为-1,结合直线AB过P0(-1,2)写出直线AB的方程,再利用点到直线的距离公式与垂径定理加以计算,即可得到弦AB的长;
(2)圆的最长的弦为直径,由此算出直线OP0的方程,即得直线AB的方程为2x+y=0;
(3)由P0为弦AB的中点,可得OP0⊥AB,因此利用直线的斜率公式算出直线AB的斜率为
,利用直线方程的点斜式列式,化简即可得到直线AB的方程x-2y+5=0.
(2)圆的最长的弦为直径,由此算出直线OP0的方程,即得直线AB的方程为2x+y=0;
(3)由P0为弦AB的中点,可得OP0⊥AB,因此利用直线的斜率公式算出直线AB的斜率为
| 1 |
| 2 |
解答:解:(1)∵直线AB的倾斜角为α,∴直线AB的斜率k=tan135°=-1,
因此,直线AB的方程为y-2=-(x+1),即x+y-1=0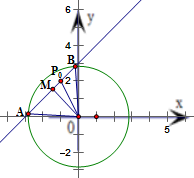
∵圆心O(0,0)到直线AB的距离d=
=
∴弦长|AB|=2
=2
=
.
(2)∵圆的最长的弦为直径,即经过圆心的弦,
∴弦AB最长时,直线AB就是以OP0确定的直线,
其方程y=-2x,可得直线AB的方程为2x+y=0;
(3)∵P0为弦AB的中点,OA=OB,∴OP0⊥AB
又∵OP0的斜率kOP0=
=-2,
∴直线AB的斜率为:kAB=
=
,
∴直线AB的方程为y-2=
(x+1),化简得x-2y+5=0.
因此,直线AB的方程为y-2=-(x+1),即x+y-1=0

∵圆心O(0,0)到直线AB的距离d=
| |-1| | ||
|
| ||
| 2 |
∴弦长|AB|=2
| r2-d2 |
8-
|
| 30 |
(2)∵圆的最长的弦为直径,即经过圆心的弦,
∴弦AB最长时,直线AB就是以OP0确定的直线,
其方程y=-2x,可得直线AB的方程为2x+y=0;
(3)∵P0为弦AB的中点,OA=OB,∴OP0⊥AB
又∵OP0的斜率kOP0=
| 2-0 |
| -1-0 |
∴直线AB的斜率为:kAB=
| -1 |
| kOP0 |
| 1 |
| 2 |
∴直线AB的方程为y-2=
| 1 |
| 2 |
点评:本题着重考查了圆的标准方程、直线的基本量与基本形式、直线与圆的位置关系和点到直线的距离公式等知识,属于中档题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目