题目内容
(本小题满分12分)
已知圆C: .
.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P( )向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
(1) y=(2±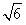 )x. (2)
)x. (2)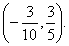
解析试题分析:解(1)将圆C配方得 .
.
① 当直线在两坐标轴上的截距为零时,设直线方程为y=kx,由直线与圆相切得 ,
,
即k=2±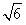 ,从而切线方程为y=(2±
,从而切线方程为y=(2±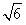 )x.
)x.
②当直线在两坐标轴上的截距不为零时,设直线方程为x+y-a=0,由直线与圆相切得x+y+1=0或x+y-3=0.
(2)由|PO|=|PM|得 得
得  .
.
即点P在直线l:2x-4y+3=0上,当|PM|取最小值时即|OP|取得最小值,直线OP⊥l,
∴直线OP的方程为2x+y=0. 解方程组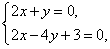 得P点坐标为
得P点坐标为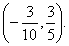
考点:本试题考查了圆的知识。
点评:对于解决圆的切线问题,一般要利用圆心到直线的距离等于圆的半径来分析,同时要对于截距的理解,注意截距都为零的情况容易丢解。同时对于距离 相等,结合切线长定理来分析最值,属于中档题。

练习册系列答案
相关题目
 ,
, 过定点
过定点 (1,0),且与圆
(1,0),且与圆 相切,求
相切,求 的半径为3,圆心在直线
的半径为3,圆心在直线 :
: 上,且与圆
上,且与圆 是圆
是圆 上的动点,
上的动点, 的取值范围;
的取值范围; 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 ,直线
,直线 :
: .
. 时,求直线
时,求直线 、
、 是单位圆
是单位圆 上的点,
上的点, 是圆与
是圆与 轴正半轴的交点,三角形
轴正半轴的交点,三角形 为正三角形, 且AB∥
为正三角形, 且AB∥
 的三个三角函数值;
的三个三角函数值; 及
及 .
. 直线
直线 .
. 相切, 且与直线
相切, 且与直线 平行的直线
平行的直线 的方程;
的方程; 与圆
与圆 轴上的截距
轴上的截距 的取值范围.
的取值范围.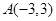 发出的光线
发出的光线 射到
射到 轴上,被
轴上,被 相切,求光线
相切,求光线 的方程
的方程 :
: .
. 为何值时,方程C表示圆。
为何值时,方程C表示圆。 相交于M,N两点,且|MN|=
相交于M,N两点,且|MN|= ,求
,求 ,使得圆上有四点到直线
,使得圆上有四点到直线 的距离为
的距离为 ,若存在,求出
,若存在,求出 的范围,若不存在,说明理由。
的范围,若不存在,说明理由。 :
: 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,过点
,过点 垂直的直线交
垂直的直线交 轴负半轴于点
轴负半轴于点 ,且
,且 .
. 三点的圆恰好与直线
三点的圆恰好与直线 :
: 相切,求椭圆
相切,求椭圆 的直线
的直线 、
、 两
两 轴上是否存在点
轴上是否存在点 使得以
使得以 为邻边的平行四边形是菱形,
为邻边的平行四边形是菱形, 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.