题目内容
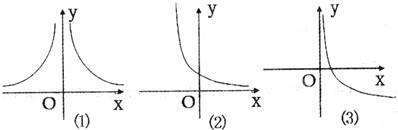
如图所示，函数y=|x|
的图象大致为（ ）
| 1 |
| 2 |
分析：可判函数为偶函数，可排除A、B，当x≥0时，f（x）=
，由幂函数的图象可得结论．
| x |
解答：解：记函数y=|x|
=f（x），
则f（-x）=|-x|
=|x|
=f（x），即函数f（x）为偶函数，
故其图象关于y轴对称，可排除A、B，
而当x≥0时，f（x）=
，由幂函数的图象可知C符合题意，
故选C
| 1 |
| 2 |
则f（-x）=|-x|
| 1 |
| 2 |
| 1 |
| 2 |
故其图象关于y轴对称，可排除A、B，
而当x≥0时，f（x）=
| x |
故选C
点评：本题考查幂函数的图象，涉及函数的奇偶性与图象的关系，属基础题．
练习册系列答案
相关题目
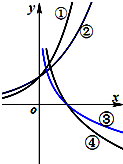如图所示为函数①y=ax、②y=bx、③y=logcx、④y=logdx的图象，其中a、b、c、d均大于0且不等于1，则 a、b、c、d大小关系为（ ）
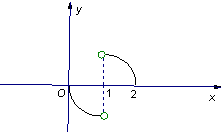如图所示，函数y=f（x）的图象是圆心在点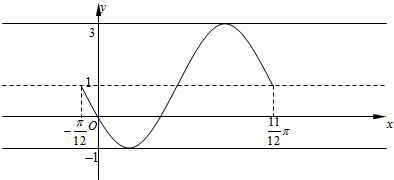
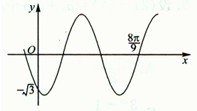如图所示，函数y=2sin（ωx+φ）（ω＞0，|φ|＜π）的图象过点