Question

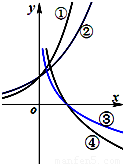
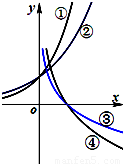
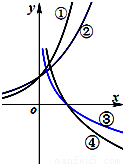
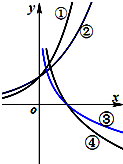如图所示为函数①y=a^x、②y=b^x、③y=log_cx、④y=log_dx的图象，其中a、b、c、d均大于0且不等于1，则 a、b、c、d大小关系为（　　）

A．a＞b＞c＞d

B．a＞b＞d＞c

C．b＞a＞c＞d

D．b＞a＞d＞c

Answer 1

分析：根据①和②都是增函数，作出直线x=1和函数①②图象的交点，可得a＞b，故a＞b＞1．根据函数③和函数④是减函数，作出直线y=1和函数③④图象的交点，可得d＞c，故有 1＞d＞c＞0，综合可得结论．

解答：解：由函数的图象可得①y=a^x 是增函数，②y=b^x是增函数，故底数a都是b大于1的实数．
作出直线x=1和函数①②图象的交点，可得a＞b，故a＞b＞1．
由函数的图象可得函数③y=log_cx 和④y=log_dx是减函数，故底数c都是d大于0且小于1的实数．
作出直线y=1和函数③④图象的交点，可得d＞c，故有 1＞d＞c＞0．
综上可得 a＞b＞d＞c，
故选B．

点评：本题主要考查函数的图象和性质，指数函数、对数函数的单调性和特殊点，以及数形结合能力，属于中档题．