题目内容
半径为r的圆的面积S(r)=πr2,周长C(r)=2πr,若将r看作(0,+∞)上的变量,则(πr2)′=2πr ①,①式可以用语言叙述为:圆的面积函数的导数等于圆的周长函数.对于半径为R的球,若将R看作(0,+∞)上的变量,请你写出类似于①的式子:分析:圆的面积函数的导数等于圆的周长函数,类比得到球的体积函数的导数等于球的表面积函数,有二维空间推广到三维空间.
解答:解:V球=
πR3,又 (
πR3)′=4πR2
用语言叙述为“球的体积函数的导数等于球的表面积函数.”
类似于①的式子可填 (
πR3)′=4πR2,
故答案为 (
πR3)′=4πR2,
| 4 |
| 3 |
| 4 |
| 3 |
用语言叙述为“球的体积函数的导数等于球的表面积函数.”
类似于①的式子可填 (
| 4 |
| 3 |
故答案为 (
| 4 |
| 3 |
点评:本题考查类比推理,解答本题的关键是:(1)找出两类事物:圆与球之间的相似性或一致性;(2)用圆的性质去推测球的性质,得出一个明确的命题(猜想).

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
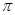 r2,周长C(r)=2
r2,周长C(r)=2