题目内容
11.已知数列{an}的前n项和为Sn,其中a1=1,Sn=3Sn-1+1(n>1,n∈N*).(1)求数列{an}的通项公式;
(2)设数列{$\frac{1}{{a}_{n}}$}的前n项和为Tn,求Tn.
分析 (1)利用递推式与等比数列的通项公式即可得出;
(2)利用等比数列的前n项和公式即可得出.
解答 解:(1)由Sn=3Sn-1+1(n>1,n∈N*)得Sn+1=3Sn+1,
∴Sn+1-Sn=3(Sn-Sn-1),即an+1=3an,(n>1,n∈N*),
又a1=1,得S2=3a1+1=a1+a2,
∴a2=3,∴$\frac{{a}_{2}}{{a}_{1}}$=3.
∴数列{an}是首项为1,公比为3的等比数列,
∴an=3n-1.
(2)∵数列{an}是首项为1,公比为3的等比数列,
∴数列{$\frac{1}{{a}_{n}}$}是首项为1,公比为$\frac{1}{3}$的等比数列,
∴Tn=$\frac{1-(\frac{1}{3})^{n}}{1-\frac{1}{3}}$=$\frac{3}{2}$[1-($\frac{1}{3}$)n].
点评 本题考查了递推式的应用、等比数列的通项公式及其前n项和公式,考查了变形能力、推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,决定从本单位中抽取50人进行问卷调查,得到了如下列联表:
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜欢户外运动与性别有关?并说明你的理由.
下面的临界值表仅供参考:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 喜欢户外运动 | 不喜欢户外运动 | 合计 | |
| 男性 | 5 | ||
| 女性 | 10 | 25 | |
| 合计 | 30 | 50 |
(2)是否有99.5%的把握认为喜欢户外运动与性别有关?并说明你的理由.
下面的临界值表仅供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
6.甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.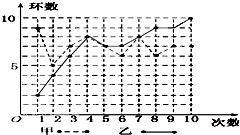
(1)请填写如表:
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看(谁的成绩更稳定);
②从折线图上两人射击命中环数的走势看(谁更有潜力).

(1)请填写如表:
| 平均数 | 方差 | 中位数 | 命中9环及9环以上的次数 | |
| 甲 | ||||
| 乙 |
①从平均数和方差相结合看(谁的成绩更稳定);
②从折线图上两人射击命中环数的走势看(谁更有潜力).
16.某中学共2200名学生中有男生1200名,按男女性别用分层抽样的方法抽出110名学生,询问是否爱好某项运动.已知男生中有40名爱好该项运动,女生中有30名不爱好该项运动.
(1)完成如下的列联表:
(2)通过计算说明,是否在犯错误的概率不超过0.01的前提下认为“爱好该项运动与性别有关”?
(1)完成如下的列联表:
| 男 | 女 | 总计 | |
| 爱好 | 40 | ||
| 不爱好 | 30 | ||
| 总计 |
1.已知随机变量X~N(0,1),则X在区间(-3,+∞)内概率为( )
| A. | 0.8874 | B. | 0.0026 | C. | 0.0013 | D. | 0.9987 |
 已知动圆P过定点A(-3,0),且与圆B:(x-3)2+y2=64相切,点P的轨迹为曲线C.设Q为曲线C上(不在x轴上)的动点,过点A作OQ的平行线交曲线C于M,N两点.
已知动圆P过定点A(-3,0),且与圆B:(x-3)2+y2=64相切,点P的轨迹为曲线C.设Q为曲线C上(不在x轴上)的动点,过点A作OQ的平行线交曲线C于M,N两点.