题目内容
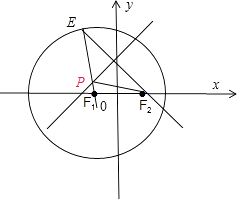
【题目】在直角坐标系xOy中,设圆的方程为(x+2 ![]() )2+y2=48,F1是圆心,F2(2
)2+y2=48,F1是圆心,F2(2 ![]() ,0)是圆内一点,E为圆周上任一点,线EF2的垂直平分线EF1的连线交于P点,设动点P的轨迹为曲线C.
,0)是圆内一点,E为圆周上任一点,线EF2的垂直平分线EF1的连线交于P点,设动点P的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)设直线l(与x轴不重合)与曲线C交于A、B两点,与x轴交于点M.
(i)是否存在定点M,使得 ![]() +
+ ![]() 为定值,若存在,求出点M坐标及定值;若不存在,请说明理由;
为定值,若存在,求出点M坐标及定值;若不存在,请说明理由;
(ii)在满足(i)的条件下,连接并延长AO交曲线C于点Q,试求△ABQ面积的最大值.
【答案】解:(Ⅰ)∵圆的方程为(x+2 ![]() )2+y2=48的圆心F1为(﹣2
)2+y2=48的圆心F1为(﹣2 ![]() ,0),半径为4
,0),半径为4 ![]() .
.
依题意点P满足 ![]() ,且4
,且4 ![]() >丨F1F2丨,
>丨F1F2丨,
故点P的轨迹为以F1、F2为焦点,长轴为4 ![]() 的椭圆
的椭圆
∴曲线C的方程: ![]() .
.

(Ⅱ)(i)设M(t,0),设直线l的方程:x=my+t,A(x1,y1),B(x2,y2),
联立 ![]() ,整理得:(m2+3)y2+2mty+t2﹣12=0,
,整理得:(m2+3)y2+2mty+t2﹣12=0,
y1+y2=﹣ ![]() ,y1y2=
,y1y2= ![]() ,
,
![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
则 ![]() +
+ ![]() =
= ![]() =
= ![]() ,
,
当2t2+24=72﹣6t2,即t2=6时, ![]() +
+ ![]() =1,
=1,
此时M的坐标为(± ![]() ,0),
,0),
综上,存在点M(± ![]() ,0),使得
,0),使得 ![]() +
+ ![]() =1,
=1,
(ii)由(i)可知:t2=6,则丨AB丨= ![]() 丨y1﹣y2丨=
丨y1﹣y2丨= ![]() ,
,
原点O直线AB的距离d= ![]() ,S△ABQ=4×
,S△ABQ=4× ![]() ×
× ![]() =
= ![]() ,
,
令 ![]() =μ∈[
=μ∈[ ![]() ,+∞),则S△ABQ=
,+∞),则S△ABQ= ![]() =
= ![]() ≤
≤ ![]() =4
=4 ![]() ,
,
当且仅当t= ![]() ,即m=0取最大值,
,即m=0取最大值,
∴△ABQ面积的最大值4 ![]()
【解析】(Ⅰ)由足 ![]() ,且4
,且4 ![]() >丨F1F2丨,则点P的轨迹为以F1、F2为焦点,长轴为4
>丨F1F2丨,则点P的轨迹为以F1、F2为焦点,长轴为4 ![]() 的椭圆,即可求得椭圆方程;(Ⅱ)(i)设直线l的方程,代入椭圆方程,由
的椭圆,即可求得椭圆方程;(Ⅱ)(i)设直线l的方程,代入椭圆方程,由 ![]() +
+ ![]() =
= ![]() ,利用韦达定理可知2t2+24=72﹣6t2,即可求得t的值,
,利用韦达定理可知2t2+24=72﹣6t2,即可求得t的值, ![]() +
+ ![]() =1;(ii)利用弦长公式,求得丨AB丨,利用点到直线距离公式,换元,即可求得△ABQ面积的最大值.
=1;(ii)利用弦长公式,求得丨AB丨,利用点到直线距离公式,换元,即可求得△ABQ面积的最大值.

【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得如表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
【题目】随着雾霾日益严重,很多地区都实行了“限行”政策,现从某地区居民中,随机抽取了300名居民了解他们对这一政策的态度,绘成如图所示的2×2列联表:
反对 | 支持 | 合计 | |
男性 | 70 | 60 | |
女性 | 50 | 120 | |
合计 |
(1)试问有没有99%的把握认为对“限行”政策的态度与性别有关?
(2)用样本估计总体,把频率作为概率,若从该地区所有的居民(人数很多)中随机抽取3人,用ξ表示所选3人中反对的人数,试写出ξ的分布列,并求出ξ的数学期望.
K2= ![]() ,其中n=a+b+c+d独立性检验临界表:
,其中n=a+b+c+d独立性检验临界表:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |