题目内容
已知函数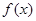 是
是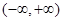 上的增函数,
上的增函数,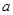 ,
,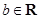 .
.
(Ⅰ)若 ,求证:
,求证: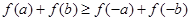 ;
;
(Ⅱ)判断(Ⅰ)中命题的逆命题是否成立,并证明你的结论.
(Ⅰ)利用函数的单调性,得,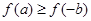 .
. 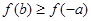 .
.
两式相加,得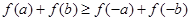 .
.
(Ⅱ)逆命题:若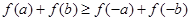 ,则
,则 .用反证法证明
.用反证法证明
解析试题分析:(Ⅰ)因为 ,所以
,所以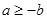 .
.
由于函数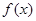 是
是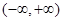 上的增函数,
上的增函数,
所以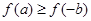 .
.
同理, 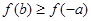 .
.
两式相加,得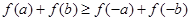 . 6分
. 6分
(Ⅱ)逆命题:
若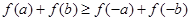 ,则
,则 .
.
用反证法证明
假设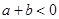 ,那么
,那么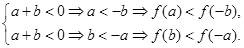
所以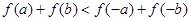 .
.
这与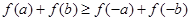 矛盾.故只有
矛盾.故只有 ,逆命题得证. 12分
,逆命题得证. 12分
考点:本题主要考查函数的单调性,反证法,命题的四种形式,不等式证明。
点评:中档题,涉及函数的不等式,往往要利用函数的单调性基本导数的性质。本题2利用反证法证明不等式要注意遵循反证法证题步骤。

练习册系列答案
相关题目
 ,
,
 的单调区间;
的单调区间; ,且
,且 ,有
,有 ,求实数
,求实数 的取值范围.
的取值范围. 在
在 与
与 时都取得极值
时都取得极值 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。 (
( )是偶函数
)是偶函数 的值;
的值; ,若函数
,若函数 与
与 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数 的取值范围
的取值范围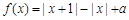 .
. 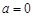 ,求不等式
,求不等式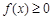 的解集;
的解集;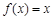 有三个不同的解,求
有三个不同的解,求 的取值范围.
的取值范围.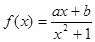 在
在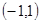 上是增函数,且
上是增函数,且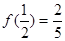
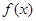 的解析式;
的解析式;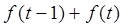 <0.
<0.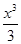 -x2-2ax(a∈R).
-x2-2ax(a∈R). 时,方程f(1-x)=
时,方程f(1-x)=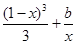 有实根,求实数b的最大值.
有实根,求实数b的最大值. 的定义域为
的定义域为 ,当
,当 时,
时, ,且对于任意的
,且对于任意的 ,恒有
,恒有 成立.
成立.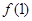 ;
; 时,
时, ;
; 上的值域.
上的值域.