题目内容
设a= ,b= (
,b= ( )2,c=
)2,c= ,则( )
,则( )
| A.a<c<b | B.b<c<a | C.a<b<c | D.b<a<c |
D
解析试题分析:由对数函数的性质可知,当底数 时,函数
时,函数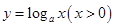 是单调增函数,
是单调增函数,
∴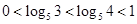 且
且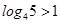 ,∴
,∴ 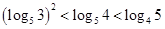 ,即
,即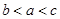 .
.
考点:对数函数的单调性及应用.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
设函数 在
在 上的导函数为
上的导函数为 ,
, 在
在 上的导函数为
上的导函数为 ,若在
,若在 上,
上, 恒成立,则称函数
恒成立,则称函数 在
在 上为“凸函数”.已知当
上为“凸函数”.已知当 时,
时, 在
在 上是“凸函数”,则
上是“凸函数”,则 在
在 上( )
上( )
| A.既没有最大值,也没有最小值 | B.既有最大值,也有最小值 |
| C.有最大值,没有最小值 | D.没有最大值,有最小值 |
已知函数 ,若
,若 ,则
,则 =( )
=( )
| A.-1 | B. | C.-1或 | D.1或- |
已知函数 ,
, ,
, ,则
,则 的最小值等于( ).
的最小值等于( ).
A. | B. | C. | D. |
如果函数 在区间
在区间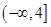 上是减函数,那么实数
上是减函数,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数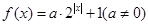 ,定义函数
,定义函数 给出下列命题:
给出下列命题:
① ; ②函数
; ②函数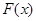 是奇函数;③当
是奇函数;③当 时,若
时,若 ,
, ,总有
,总有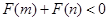 成立,其中所有正确命题的序号是( )
成立,其中所有正确命题的序号是( )
| A.② | B.①② | C.③ | D.②③ |
下列大小关系正确的是( )
A. | B. |
C. | D. |
 则
则 的大致图象是( )
的大致图象是( )
 在区间
在区间 上是减函数,则a的取值范围是( ).
上是减函数,则a的取值范围是( ).  B.
B. C
C D.
D.