题目内容
12．求x的值：logx（3+2$\sqrt{2}$）=-2．分析 利用对数，指数式的转化得出x-2=3$+2\sqrt{2}$=（$\sqrt{2}+1$）2，x＞0，x≠1，求解即可．
解答 解：∵logx（3+2$\sqrt{2}$）=-2．
∴x-2=3$+2\sqrt{2}$=（$\sqrt{2}+1$）2，x＞0，x≠1，
即x=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}-1$．
点评 本题考查了对数，指数式的联系转化，属于简单的计算题目，准确计算即可．
练习册系列答案
相关题目
4．下列说法正确的是（ ）
| A． | 命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1” | |
| B． | 命题“?x0∈R，x${\;}_{0}^{2}$+x0-1＜0”的否定是“?x∈R，x2+x-1＞0” | |
| C． | 命题“若x=y，则sin x=sin y”的逆否命题为假命题 | |
| D． | 若“p或q”为真命题，则p，q中至少有一个为真命题 |
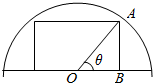如图所示，在一住宅小区里有一块半径为10m的半圆形空地（O为圆心），现准备在这块空地上种植一块矩形草坪，矩形的一边落在半圆的直径上，问角θ为多少度时，矩形草坪面积最大？并求出最大面积．